Ôn tập chương 2 - Sóng cơ và sóng âm

Ta có điều kiện sóng dừng trên dây hai đầu cố định: $l = k\frac{\lambda }{2} = k\frac{v}{{2f}}$

Ta suy ra: $f = k\frac{v}{{2l}}$

Mặt khác, ta có $k = 1$ ứng với âm cơ bản

=> Tần số của âm cơ bản do dây đàn phát ra bằng: ${f_1} = \frac{v}{{2l}}$

Ta có:

+ Khoảng cách từ gợn sóng thứ nhất đến gợn sóng thứ $5$ là: $4\lambda  = 0,5m \to \lambda  = \frac{{0,5}}{4} = 0,125m$

+ Tốc độ truyền sóng là: $v = \lambda f = 0,125.120 = 15m/s$

+ Khoảng cách giữa hai điểm gần nhau nhất trên cùng hướng truyền sóng dao động vuông pha với nhau nên ta có: $\Delta \varphi  = \frac{{2\pi d}}{\lambda } = \frac{\pi }{2} \to \frac{d}{\lambda } = \frac{1}{4} \to \lambda  = 4d$  (1)

+ Tần số của âm: $f = \frac{v}{\lambda }$  (2)

Từ (1) và (2), ta suy ra: $f = \frac{v}{{4d}}$

Ta có, tần số âm của lá thép là: $f = \frac{1}{T} = \frac{1}{{{{80.10}^{ - 3}}}} = 12,5Hz < 16Hz$

=> Âm mà lá thép phát ra là hạ âm

Gọi

+ Thời gian máy địa chấn ghi được tín hiệu từ cơn động đất do sóng (N) và sóng (D) truyền đến lần lượt là: ${t_1}$ và ${t_2}$

+ Khoảng cách từ tâm động đất đến máy địa chấn là: $s$

Vận tốc của sóng (N) là: ${v_1} = 34,5km/s$

Vận tốc của sóng (D) là: ${v_2} = 8km/s$

Ta có quãng đường truyền của hai sóng là như nhau (đều từ tâm động đất đến máy địa chấn) và bằng $s$

Ta suy ra:

$\left\{ \begin{array}{l}{t_1} = \dfrac{s}{{{v_1}}} = \dfrac{s}{{34,5}}\\{t_2} = \dfrac{s}{{{v_2}}} = \dfrac{s}{{8}}\end{array} \right.$

Mặt khác, theo đề bài ta có sóng (N) đến sớm hơn sóng (D):

$4$ phút $= 4.60 = 240$ giây, ta có:

$\begin{array}{l}{t_2} - {t_1} = 240\\ \leftrightarrow \dfrac{s}{8} - \dfrac{s}{{34,5}} = 240 \leftrightarrow \dfrac{{53s}}{{552}} = 240\\ \to s = 2499,6km \approx 2500km\end{array}$

Ta có: ${L_A} = 50dB,{L_B} = 30dB$

Hiệu mức cường độ âm:

$\begin{array}{l}{L_A} - {L_B} = 10\log \dfrac{{r_B^2}}{{r_A^2}} = 10\log \dfrac{{O{B^2}}}{{O{A^2}}} = 50 - 30 = 20\\ \leftrightarrow \log \dfrac{{O{B^2}}}{{O{A^2}}} = 2 \to O{B^2} = {10^2}O{A^2}\\ \to OB = 10OA\end{array}$

 Ta có: ${r_M} = OM = OB - MB = OB - \dfrac{{(OB - OA)}}{2} = \dfrac{{OB + OA}}{2} = \dfrac{{11OA}}{2}$

$\begin{array}{l}{L_A} - {L_M} = 10\log \dfrac{{r_M^2}}{{r_A^2}} = 10\log \dfrac{{{{\left( {\dfrac{{11OA}}{2}} \right)}^2}}}{{O{A^2}}} = 14,8\\ \to {L_M} = 50 - 14,8 = 35,2dB\end{array}$

Mặt khác, ta có:

$\begin{array}{l}{L_M} = 10\log \dfrac{{{I_M}}}{{{I_0}}} = 35,2dB\\ \to \log \dfrac{{{I_M}}}{{{I_0}}} = 3,52\\ \to {I_M} = {I_0}{.10^{3,52}} = {10^{ - 12}}{.10^{3,52}} = {3,3.10^{ - 9}}{\rm{W}}/{m^2}\end{array}$

Từ phương trình sóng: $u = 4\cos \left( {\frac{{\pi t}}{3} + \frac{{\pi x}}{6} - \frac{\pi }{3}} \right)cm$, ta có:

Pha dao động: $\frac{{\pi t}}{3} - \frac{\pi }{3} + \frac{{\pi x}}{6}$ => Sóng truyền theo chiều âm của trục Ox

$\frac{{2\pi x}}{\lambda } = \frac{{\pi x}}{6} \to \lambda  = 12m$

Tốc độ truyền sóng: $v = \frac{\lambda }{T} = \frac{\lambda }{{\frac{{2\pi }}{\omega }}} = \frac{{\lambda \omega }}{{2\pi }} = \frac{{12.\frac{\pi }{3}}}{{2\pi }} = 2m/s = 200cm/s$

Vậy sóng truyền theo chiều âm của trục Ox với tốc độ $200cm/s$

Ta có:

+ Khoảng cách giữa hai điểm dao động với biên độ cực đại cách nhau một khoảng ngắn nhất là: $\frac{\lambda }{2} = 2cm \to \lambda  = 4cm$

+ Tốc độ truyền sóng: $v = \frac{\lambda }{T} = \frac{\lambda }{{\frac{{2\pi }}{\omega }}} = \frac{4}{{\frac{{2\pi }}{{25\pi }}}} = 50cm/s$

Khoảng thời gian để sóng truyền được quãng đường bằng một bước sóng là một chu kỳ

Ta có khoảng cách giữa hai cực tiểu giao thoa liên tiếp là $\dfrac{\lambda }{2} = 0,5cm$

=> sóng truyền trên mặt nước có bước sóng là $\lambda  = 0,5.2 = 1cm$

Ta có, bước sóng $\lambda  = \frac{v}{f} = \frac{5}{5} = 1m$

Ta có, mức cường độ âm: $L = \log \frac{I}{{{I_0}}} = \log \frac{{{{10}^{ - 5}}}}{{{{10}^{ - 12}}}} = 7B = 70dB$

Ta có:

+ Bước sóng: $\lambda  = \frac{v}{f} = \frac{4}{{50}} = 0,08m = 8cm$

+ Mặt khác, ta có dây hai đầu cố định => chiều dài dây: $l = n\frac{\lambda }{2}$

Thay vào ta được: $32 = n\frac{8}{2} \to n = 8$

=> Trên dây có 8 bụng và 9 nút

Từ phương trình sóng: $u = Acos\left( {20\pi t--\pi x} \right){\rm{ }}\left( {cm} \right)$

Ta suy ra, tần số góc $\omega  = 20\pi$

$\to f = \frac{\omega }{{2\pi }} = 10Hz$

Những điểm thuộc vân giao thoa cực tiểu có biên độ dao động bằng 0

$OH$ là đường cao hạ từ $O$ xuống

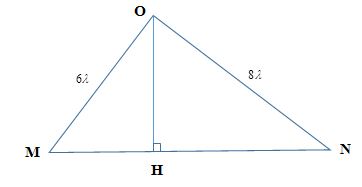
+ Ta có:

$\begin{array}{l}\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{M^2}}} + \dfrac{1}{{O{N^2}}} = \dfrac{1}{{{6^2}}} + \dfrac{1}{{{8^2}}} = \dfrac{{25}}{{576}}\\ \to OH = 4,8\lambda \end{array}$

+ Các điểm trên $MN$ ngược pha với nguồn thỏa mãn $d = (k + 0,5)\lambda$ ta xác định được

- Trong khoảng $HM$, ta có:

$\begin{array}{l}OH \le d \le OM\\ \Leftrightarrow 4,8\lambda  \le \left( {k + 0,5} \right)\lambda  \le 6\lambda \\ \Leftrightarrow 4,3 \le k \le 5,5\end{array}$

=> có $1$ điểm ứng với $k = 5$

- Trong khoảng $HN$, ta có:

$\begin{array}{l}OH \le d \le ON\\ \Leftrightarrow 4,8\lambda  \le \left( {k + 0,5} \right)\lambda  \le 8\lambda \\ \Leftrightarrow 4,3 \le k \le 7,5\end{array}$

=> có $3$ điểm ứng với $k = 5,6,7$

Vậy trên đoạn thẳng $MN$, có 4 điểm mà tại đó các phần tử nước dao động ngược pha với dao động của nguồn $O$

Sóng cơ chỉ truyền được trong các môi trường rắn , lỏng, khí

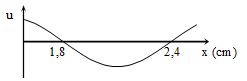
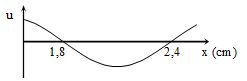
Từ đồ thị, ta thấy, khoảng cách giữa hai nút liên tiếp là một nửa bước sóng

=> $2,4 - 1,8 = \frac{\lambda }{2} = 0,6 \to \lambda  = 1,2cm$

$M$ là cực đại giao thoa và ngược pha với hai nguồn, ta có:

+ Điều kiện cực đại giao thoa của hai nguồn cùng pha: ${d_1} - {d_2} = k\lambda$

+ Điều kiện dao động ngược pha với nguồn: ${d_1} - {d_2} = \left( {2k + 1} \right)\lambda$

=>  $\left\{ \begin{array}{l}{d_1} - {d_2} = n\lambda \\{d_1} + {d_2} = m\lambda \end{array} \right.(1)$  n và m là số nguyên n lẻ, m chẵn

Theo đề bài ta có : ${d_1} - {d_2} = MA - MB = \lambda$
Vì  $n{\rm{ }} = {\rm{ }}1$

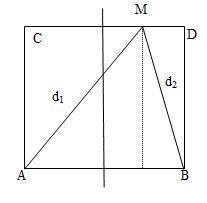
Trên hình, theo đề ta có :$\left\{ \begin{array}{l}{d_1} + {d_2} > 2AB\\4\lambda  \le AB < 5\lambda \end{array} \right.\left( 2 \right)$

Từ (1) và (2) => $\left\{ \begin{array}{l}{d_1} - {d_2} = \lambda \\{d_1} + {d_2} = 10\lambda \end{array} \right. \Rightarrow \left\{ \begin{array}{l}{d_1} = 5,5\lambda \\{d_2} = 4,5\lambda \end{array} \right..$

$\sqrt {{{5,5}^2}{\lambda ^2} - A{B^2}}  + \sqrt {{{4,5}^2}\lambda  - A{B^2}}  = AB \to AB = 4,376749\lambda$

Gọi ${f_1}$  là tần số âm cơ bản

=> $2640Hz$  và $4400Hz$  phải chia hết cho ${f_1}$

=> ${f_1}$ là ước chung của $2640$ và $4400$

Ta có, ước chung lớn nhất của $2640$ và $4400$ là $880$

=> ${f_1}$ là ước của $880$

Lại có $300 < {f_1} < 800$

Từ đó, ta suy ra : ${f_1} = 440Hz$

Họa âm của âm : ${f_n} = n{f_1}$

Trong vùng tần số của âm nghe được $16Hz - 20000Hz$,

$\begin{array}{l}16 < 440n < 20000\\ \leftrightarrow 0,036 < n < 45,45\\ \to n = 1,2,...,45\end{array}$

=> Có 45 họa âm kể cả âm cơ bản