Ở mặt nước, một nguồn sóng đặt tại \(O\) dao động điều hòa theo phương thẳng đứng. Sóng truyền trên mặt nước với bước sóng \(\lambda \). \(M\) và \(N\) là hai điểm ở mặt nước sao cho \(OM = 6\lambda ,ON = 8\lambda \) và \(OM\) vuông góc với \(ON\). Trên đoạn thẳng \(MN\), số điểm mà tại đó các phần tử nước dao động ngược pha với dao động của nguồn \(O\) là:
Trả lời bởi giáo viên
\(OH\) là đường cao hạ từ \(O\) xuống
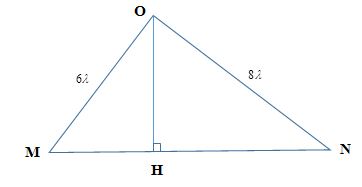
+ Ta có:
\(\begin{array}{l}\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{M^2}}} + \dfrac{1}{{O{N^2}}} = \dfrac{1}{{{6^2}}} + \dfrac{1}{{{8^2}}} = \dfrac{{25}}{{576}}\\ \to OH = 4,8\lambda \end{array}\)
+ Các điểm trên \(MN\) ngược pha với nguồn thỏa mãn \(d = (k + 0,5)\lambda \) ta xác định được
- Trong khoảng \(HM\), ta có:
\(\begin{array}{l}OH \le d \le OM\\ \Leftrightarrow 4,8\lambda \le \left( {k + 0,5} \right)\lambda \le 6\lambda \\ \Leftrightarrow 4,3 \le k \le 5,5\end{array}\)
=> có \(1\) điểm ứng với \(k = 5\)
- Trong khoảng \(HN\), ta có:
\(\begin{array}{l}OH \le d \le ON\\ \Leftrightarrow 4,8\lambda \le \left( {k + 0,5} \right)\lambda \le 8\lambda \\ \Leftrightarrow 4,3 \le k \le 7,5\end{array}\)
=> có \(3\) điểm ứng với \(k = 5,6,7\)
Vậy trên đoạn thẳng \(MN\), có 4 điểm mà tại đó các phần tử nước dao động ngược pha với dao động của nguồn \(O\)
Hướng dẫn giải:
+ Sử dụng hệ thức lượng trong tam giác vuông
+ Sử dụng điều kiện dao động ngược pha: \(d = \left( {k + \frac{1}{2}} \right)\lambda \)

