Số đo cung \(CD\) nhỏ và số đo cung \(CD\) lớn lần lượt là
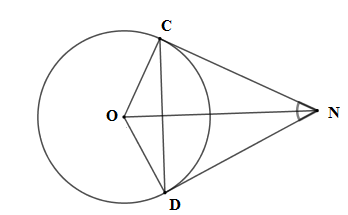
Xét tứ giác $ODNC$ có \(\widehat {COD} + \widehat {OCN} + \widehat {CND} + \widehat {ODN} = 360^\circ \)
$ \Rightarrow \widehat {COD} = 360^\circ - \widehat {OCN} - \widehat {ODN} - \widehat {CND} = 360^\circ - 90^\circ - 90^\circ - 60^\circ = 120^\circ $
Suy ra số đo cung nhỏ $CD$ là $120^\circ $; số đo cung lớn $CD$ là $360^\circ - 120^\circ = 240^\circ $.
Tính \(\widehat {DNO}\) và \(\widehat {CON}\)
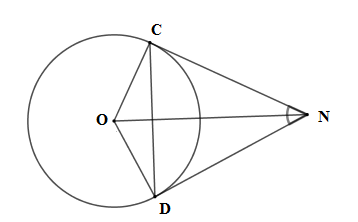
Vì $NC,ND$ là hai tiếp tuyến của đường tròn $\left( O \right)$ nên $ON$ là tia phân giác của $\widehat {COD}$; $NO$ là tia phân giác của $\widehat {CND}$ hay $\widehat {DNO} = \dfrac{1}{2}\widehat {DMC} = \dfrac{{60^\circ }}{2} = 30^\circ $.
Mà tam giác $ODN$ vuông tại $D$ (do $ND$ là tiếp tuyến) nên $\widehat {DON} = 90^\circ - \widehat {DNO} = 90^\circ - 30^\circ = 60^\circ $
Mà $ON$ là tia phân giác của $\widehat {COD}$ nên $\widehat {NOC} = \widehat {NOD} = 60^\circ $.
Vậy $\widehat {DNO} = 30^\circ ;\widehat {NOC} = 60^\circ $
Tính \(\widehat {DNO}\) và \(\widehat {CON}\)

Vì $NC,ND$ là hai tiếp tuyến của đường tròn $\left( O \right)$ nên $ON$ là tia phân giác của $\widehat {COD}$; $NO$ là tia phân giác của $\widehat {CND}$ hay $\widehat {DNO} = \dfrac{1}{2}\widehat {DMC} = \dfrac{{60^\circ }}{2} = 30^\circ $.
Mà tam giác $ODN$ vuông tại $D$ (do $ND$ là tiếp tuyến) nên $\widehat {DON} = 90^\circ - \widehat {DNO} = 90^\circ - 30^\circ = 60^\circ $
Mà $ON$ là tia phân giác của $\widehat {COD}$ nên $\widehat {NOC} = \widehat {NOD} = 60^\circ $.
Vậy $\widehat {DNO} = 30^\circ ;\widehat {NOC} = 60^\circ $
Cho tam giác $ABC$ đều nội tiếp đường tròn $\left( O \right)$. Tính số đo cung $BC$ nhỏ.
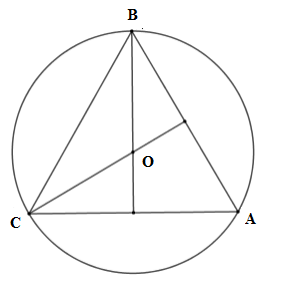
Vì tam giác $ABC$ đều có $O$ là tâm đường tròn ngoại tiếp nên $O$ cũng là giao ba đường phân giác nên $BO;CO$ lần lượt là các đường phân giác $\widehat {ABC}$; $\widehat {ACB}$.
Ta có $\widehat {BCO} = \dfrac{1}{2}\widehat {ACB} = \dfrac{{60^\circ }}{2} = 30^\circ $;$\widehat {CBO} = \dfrac{1}{2}\widehat {ABC} = \dfrac{{60^\circ }}{2} = 30^\circ $
Xét tam giác $BOC$ có $\widehat {BOC} = 180^\circ - \widehat {CBO} - \widehat {BCO} = 180^\circ - 30^\circ - 30^\circ = 120^\circ $
Do đó số đo cung nhỏ \(BC\) là \(120^\circ .\)
Số đo cung \(AB\) lớn là
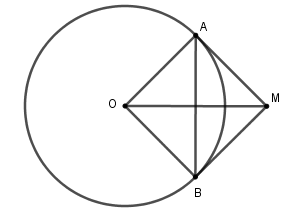
Theo câu trước ta có \(\widehat {BMO} = 45^\circ \) . Xét tam giác \(OBM\) vuông tại \(B\) (do \(BM\) là tiếp tuyến của \(\left( O \right)\)) có \(\widehat {BMO} = 45^\circ \Rightarrow \widehat {BOM} = 90^\circ - 45^\circ = 45^\circ \)
Xét đường tròn $\left( O \right)$ có $MA;MB$ là hai tiếp tuyến cắt nhau tại $M$ nên $OM$ là tia phân giác của góc $\widehat {AOB}$
Suy ra $\widehat {AOB} = 2\widehat {BOM} = 2.45^\circ = 90^\circ $ mà $\widehat {AOB}$ là góc ở tâm chắn cung \(AB\)
Nên số đo cung nhỏ \(AB\) là $90^\circ $ suy ra số đo cung lớn \(AB\) là \(360^\circ - 90^\circ = 270^\circ \) .
Số đo góc $\widehat {BMO}$ là
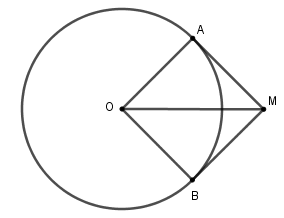
Xét tam giác $AOB$ vuông tại $A$ ta có $\sin \widehat {BMO} = \dfrac{{OB}}{{OM}} = \dfrac{R}{{\sqrt 2 R}} = \dfrac{1}{{\sqrt 2 }} \Rightarrow \widehat {BMO} = 45^\circ $
Số đo góc $\widehat {BMO}$ là

Xét tam giác $AOB$ vuông tại $A$ ta có $\sin \widehat {BMO} = \dfrac{{OB}}{{OM}} = \dfrac{R}{{\sqrt 2 R}} = \dfrac{1}{{\sqrt 2 }} \Rightarrow \widehat {BMO} = 45^\circ $
Tính số đo cung nhỏ $MN$
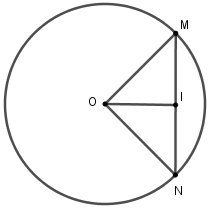
Xét tam giác $OIM$ vuông tại $I$ ta có $\sin \widehat {MOI} = \dfrac{{MI}}{{MO}} = \dfrac{{\sqrt 2 R}}{2}:R = \dfrac{{\sqrt 2 }}{2} \Rightarrow \widehat {MOI} = 45^\circ $
$\Delta MON$ cân tại $O$ có $OI$ vừa là đường cao vừa là đường phân giác nên $\widehat {MON} = 2\widehat {MOI} = 2.45^\circ = 90^\circ $
Suy ra số đo cung nhỏ $MN$ là $90^\circ $.
Tính độ dài \(OI\) theo $R$ .
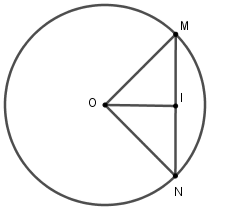
Xét $\left( O \right)$ có $OI \bot MN$ tại $I$ nên $I$ là trung điểm của $MN$ $ \Rightarrow MI = IN = \dfrac{{\sqrt 2 R}}{2}$
Xét tam giác $OIM$ vuông tại $I$, theo định lý Pytago ta có $O{I^2} = O{M^2} - M{I^2} \Rightarrow OI = \sqrt {{R^2} - {{\left( {\dfrac{{\sqrt 2 R}}{2}} \right)}^2}} = \dfrac{{\sqrt 2 R}}{2}$
Tính độ dài \(OI\) theo $R$ .

Xét $\left( O \right)$ có $OI \bot MN$ tại $I$ nên $I$ là trung điểm của $MN$ $ \Rightarrow MI = IN = \dfrac{{\sqrt 2 R}}{2}$
Xét tam giác $OIM$ vuông tại $I$, theo định lý Pytago ta có $O{I^2} = O{M^2} - M{I^2} \Rightarrow OI = \sqrt {{R^2} - {{\left( {\dfrac{{\sqrt 2 R}}{2}} \right)}^2}} = \dfrac{{\sqrt 2 R}}{2}$
Tính $\widehat {IOK}$ biết $\widehat {BAC} = 36^\circ $
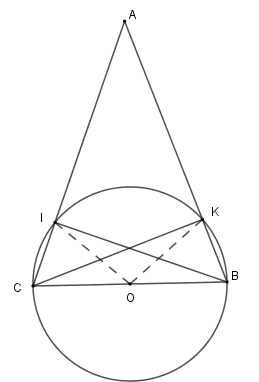
Xét tam giác $ABC$ cân tại $A$ có $\widehat A = 36^\circ \Rightarrow \widehat {KBO} = \widehat {ICO} = \dfrac{{180^\circ - 36^\circ }}{2} = 72^\circ $
Xét tam giác $OKB$cân tại $O$ có $\widehat {KBO} = 72^\circ \Rightarrow \widehat {KOB} = 180^\circ - 2.72^\circ = 36^\circ $
Theo câu trước ta có $\widehat {IOC} = \widehat {KOB} = 36^\circ $
Suy ra $\widehat {IOK} = 180^\circ - 36^\circ - 36^\circ = 108^\circ $.
So sánh các cung nhỏ $CI$ và cung nhỏ $BK$
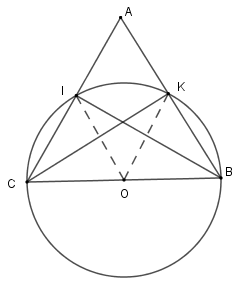
Xét các tam giác $\Delta IBC$ và $\Delta KBC$ có $BC$ là đường kính của $\left( O \right)$ và $I;K \in \left( O \right)$
Nên $\Delta IBC$ vuông tại $I$ và $\Delta KBC$ vuông tại $K$
Xét hai tam giác vuông $\Delta IBC$ và $\Delta KBC$ ta có $BC$ chung; $\widehat {ABC} = \widehat {ABC}$ (do$\Delta ABC$ cân)
$ \Rightarrow \Delta IBC = \Delta KCB\left( {ch - gn} \right) \Rightarrow IC = BK$ (hai cạnh tương ứng)
Suy ra $\Delta COI = \Delta {\rm B}OK\left( {c - c - c} \right)$$ \Rightarrow \widehat {COI} = \widehat {KOB}$ suy ra số đo hai cung nhỏ $CI$ và $BK$ bằng nhau.
So sánh các cung nhỏ $CI$ và cung nhỏ $BK$

Xét các tam giác $\Delta IBC$ và $\Delta KBC$ có $BC$ là đường kính của $\left( O \right)$ và $I;K \in \left( O \right)$
Nên $\Delta IBC$ vuông tại $I$ và $\Delta KBC$ vuông tại $K$
Xét hai tam giác vuông $\Delta IBC$ và $\Delta KBC$ ta có $BC$ chung; $\widehat {ABC} = \widehat {ABC}$ (do$\Delta ABC$ cân)
$ \Rightarrow \Delta IBC = \Delta KCB\left( {ch - gn} \right) \Rightarrow IC = BK$ (hai cạnh tương ứng)
Suy ra $\Delta COI = \Delta {\rm B}OK\left( {c - c - c} \right)$$ \Rightarrow \widehat {COI} = \widehat {KOB}$ suy ra số đo hai cung nhỏ $CI$ và $BK$ bằng nhau.
Cho đường tròn \(\left( {O;R} \right).\) Gọi \(H\) là điểm thuộc bán kính \(OA\) sao cho \(OH = \dfrac{{\sqrt 3 }}{2}OA\) . Dây \(CD\) vuông góc với \(OA\) tại $H.$ Tính số đo cung lớn \(CD.\)
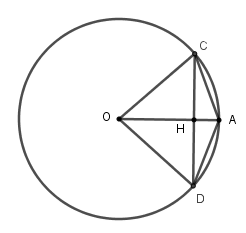
Xét đường tròn$\left( O \right)$ có $OA \bot CD$ tại $H$ nên $H$ là trung điểm của $CD.$
Xét tam giác \(OHC\) vuông tại \(H\) có \(\cos \widehat {HOC} = \dfrac{{OH}}{{OC}} = \dfrac{{\dfrac{{\sqrt 3 R}}{2}}}{R} = \dfrac{{\sqrt 3 }}{2} \Rightarrow \widehat {HOC} = 30^\circ \)
Mà tam giác \(OCD\) cân tại \(O\left( {OC = OD = R} \right)\) có \(OH\) là đường cao nên \(OH\) cũng là đường phân giác, suy ra \(\widehat {DOC} = 2.\widehat {COH} = 2.30^\circ = 60^\circ \)
Do đó số đo cung nhỏ $CD$ là $60^\circ $ và số đo cung lớn $CD$ là $360^\circ - 60^\circ = 300^\circ $.
Chọn khẳng định đúng. Góc ở tâm là góc
Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm.
Chọn khẳng định đúng. Trong một đường tròn, số đo cung nhỏ bằng
Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
Trong hai cung của một đường tròn hay hai đường tròn bằng nhau, cung nào nhỏ hơn
Trong hai cung của một đường tròn hay hai đường tròn bằng nhau, cung nào nhỏ hơn thì có số đo nhỏ hơn.
Cho hai tiếp tuyến tại $A$ và $B$ của đường tròn \(\left( O \right)\) cắt nhau tại M, biết \(\widehat {AMB} = {50^0}\) .
Tính \(\widehat {AMO}\) và \(\widehat {BOM}\)
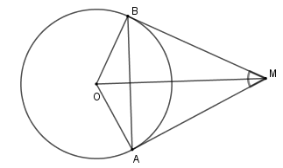
Vì $MA,MB$ là hai tiếp tuyến của đường tròn $\left( O \right)$ nên $OM$ là tia phân giác của $\widehat {AOB}$; $MO$ là tia phân giác của $\widehat {AMB}$ hay $\widehat {AMO} = \dfrac{1}{2}\widehat {AMB} = \dfrac{{50^\circ }}{2} = 25^\circ $.
Mà tam giác $OAM$ vuông tại $A$ (do $MA$ là tiếp tuyến) nên $\widehat {MOA} = 90^\circ - \widehat {AMO} = 65^\circ $
Mà $OM$ là tia phân giác của $\widehat {AOB}$ nên $\widehat {MOB} = \widehat {MOA} = 65^\circ $.
Vậy $\widehat {AMO} = 25^\circ ;\widehat {MOB} = 65^\circ. $
Cho hai tiếp tuyến tại $A$ và $B$ của đường tròn \(\left( O \right)\) cắt nhau tại M, biết \(\widehat {AMB} = {50^0}\) .
Số đo cung \(AB\) nhỏ và số đo cung \(AB\) lớn lần lượt là
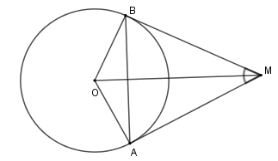
Xét tứ giác $OAMB$ có
$\widehat {BOA} + \widehat {OBM} + \widehat {OAM} + \widehat {AMB} = 360^\circ \Rightarrow \widehat {BOA} = 360^\circ - 90^\circ - 90^\circ - 50^\circ = 130^\circ $
Suy ra số đo cung nhỏ $AB$ là $130^\circ $; số đo cung lớn $AB$ là $360^\circ - 130^\circ = 230^\circ $.
Cho tam giác $ABC$ đều nội tiếp đường tròn $\left( O \right)$. Tính số đo cung $AC$ lớn.
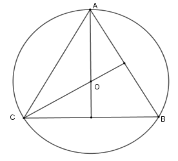
Vì tam giác $ABC$ đều có $O$ là tâm đường tròn ngoại tiếp nên $O$ cũng là giao ba đường phân giác nên $AO;CO$ lần lượt là các đường phân giác $\widehat {BAC}$; $\widehat {ACB}$.
Ta có $\widehat {CAO} = \dfrac{1}{2}\widehat {BAC} = \dfrac{{60^\circ }}{2} = 30^\circ $;$\widehat {ACO} = \dfrac{1}{2}\widehat {ACB} = \dfrac{{60^\circ }}{2} = 30^\circ $
Xét tam giác $AOC$ có $\widehat {AOC} = 180^\circ - \widehat {CAO} - \widehat {ACO} = 120^\circ $ nên số đo cung nhỏ $AC$ là $120^\circ $.
Do đó số đo cung lớn $AC$ là $360^\circ - 120^\circ = 240^\circ $.

