Trả lời bởi giáo viên
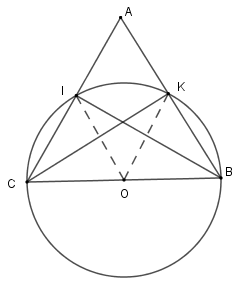
Xét các tam giác $\Delta IBC$ và $\Delta KBC$ có $BC$ là đường kính của $\left( O \right)$ và $I;K \in \left( O \right)$
Nên $\Delta IBC$ vuông tại $I$ và $\Delta KBC$ vuông tại $K$
Xét hai tam giác vuông $\Delta IBC$ và $\Delta KBC$ ta có $BC$ chung; $\widehat {ABC} = \widehat {ABC}$ (do$\Delta ABC$ cân)
$ \Rightarrow \Delta IBC = \Delta KCB\left( {ch - gn} \right) \Rightarrow IC = BK$ (hai cạnh tương ứng)
Suy ra $\Delta COI = \Delta {\rm B}OK\left( {c - c - c} \right)$$ \Rightarrow \widehat {COI} = \widehat {KOB}$ suy ra số đo hai cung nhỏ $CI$ và $BK$ bằng nhau.
Hướng dẫn giải:
Sử dụng tam giác bằng nhau
So sánh hai cung:
Trong một đường tròn hay hai đường tròn bằng nhau:
- Hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau.
- Trong hai cung, cung nào có số đo lớn hơn được gọi là cung lớn hơn.

