Câu hỏi:
2 năm trước
Cho hai tiếp tuyến tại $A$ và $B$ của đường tròn \(\left( O \right)\) cắt nhau tại M, biết \(\widehat {AMB} = {50^0}\) .
Tính \(\widehat {AMO}\) và \(\widehat {BOM}\)
Trả lời bởi giáo viên
Đáp án đúng: c
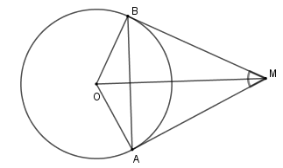
Vì $MA,MB$ là hai tiếp tuyến của đường tròn $\left( O \right)$ nên $OM$ là tia phân giác của $\widehat {AOB}$; $MO$ là tia phân giác của $\widehat {AMB}$ hay $\widehat {AMO} = \dfrac{1}{2}\widehat {AMB} = \dfrac{{50^\circ }}{2} = 25^\circ $.
Mà tam giác $OAM$ vuông tại $A$ (do $MA$ là tiếp tuyến) nên $\widehat {MOA} = 90^\circ - \widehat {AMO} = 65^\circ $
Mà $OM$ là tia phân giác của $\widehat {AOB}$ nên $\widehat {MOB} = \widehat {MOA} = 65^\circ $.
Vậy $\widehat {AMO} = 25^\circ ;\widehat {MOB} = 65^\circ. $
Hướng dẫn giải:
Sử dụng tính chất hai tiếp tuyến cắt nhau

