Trả lời bởi giáo viên
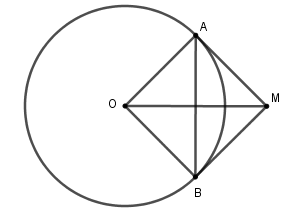
Theo câu trước ta có \(\widehat {BMO} = 45^\circ \) . Xét tam giác \(OBM\) vuông tại \(B\) (do \(BM\) là tiếp tuyến của \(\left( O \right)\)) có \(\widehat {BMO} = 45^\circ \Rightarrow \widehat {BOM} = 90^\circ - 45^\circ = 45^\circ \)
Xét đường tròn $\left( O \right)$ có $MA;MB$ là hai tiếp tuyến cắt nhau tại $M$ nên $OM$ là tia phân giác của góc $\widehat {AOB}$
Suy ra $\widehat {AOB} = 2\widehat {BOM} = 2.45^\circ = 90^\circ $ mà $\widehat {AOB}$ là góc ở tâm chắn cung \(AB\)
Nên số đo cung nhỏ \(AB\) là $90^\circ $ suy ra số đo cung lớn \(AB\) là \(360^\circ - 90^\circ = 270^\circ \) .
Hướng dẫn giải:
Sử dụng tính chất hai tiếp tuyến cắt nhau và số đo cung: “Số đo cung nhỏ bằng số đo góc ở tâm chắn cung đó”
“Số đo cung lớn bằng hiệu của \(360^\circ \) và số đo của cung nhỏ (có chung $2$ mút với cung lớn)”

