Trả lời bởi giáo viên
Đáp án đúng: d
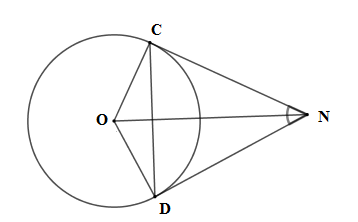
Vì NC,ND là hai tiếp tuyến của đường tròn (O) nên ON là tia phân giác của ^COD; NO là tia phân giác của ^CND hay ^DNO=12^DMC=60∘2=30∘.
Mà tam giác ODN vuông tại D (do ND là tiếp tuyến) nên ^DON=90∘−^DNO=90∘−30∘=60∘
Mà ON là tia phân giác của ^COD nên ^NOC=^NOD=60∘.
Vậy ^DNO=30∘;^NOC=60∘
Hướng dẫn giải:
Sử dụng tính chất hai tiếp tuyến cắt nhau và tính chất tia phân giác của một góc

