Trả lời bởi giáo viên
Đáp án đúng: c
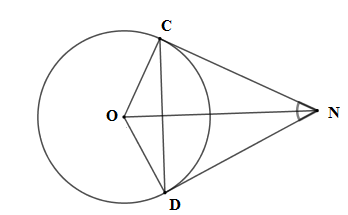
Xét tứ giác ODNC có ^COD+^OCN+^CND+^ODN=360∘
⇒^COD=360∘−^OCN−^ODN−^CND=360∘−90∘−90∘−60∘=120∘
Suy ra số đo cung nhỏ CD là 120∘; số đo cung lớn CD là 360∘−120∘=240∘.
Hướng dẫn giải:
Sử dụng định lý tổng các góc trong tứ giác bằng 360∘ và số đo cung.
Trong một đường tròn
- Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
- Số đo của cung lớn bằng hiệu giữa 3600 và số đo của cung nhỏ (có chung 2 mút với cung lớn).

