Câu hỏi:
2 năm trước
Cho đường tròn \(\left( {O;R} \right).\) Gọi \(H\) là điểm thuộc bán kính \(OA\) sao cho \(OH = \dfrac{{\sqrt 3 }}{2}OA\) . Dây \(CD\) vuông góc với \(OA\) tại $H.$ Tính số đo cung lớn \(CD.\)
Trả lời bởi giáo viên
Đáp án đúng: b
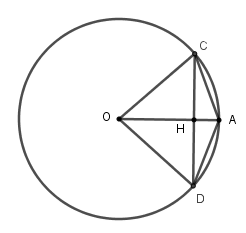
Xét đường tròn$\left( O \right)$ có $OA \bot CD$ tại $H$ nên $H$ là trung điểm của $CD.$
Xét tam giác \(OHC\) vuông tại \(H\) có \(\cos \widehat {HOC} = \dfrac{{OH}}{{OC}} = \dfrac{{\dfrac{{\sqrt 3 R}}{2}}}{R} = \dfrac{{\sqrt 3 }}{2} \Rightarrow \widehat {HOC} = 30^\circ \)
Mà tam giác \(OCD\) cân tại \(O\left( {OC = OD = R} \right)\) có \(OH\) là đường cao nên \(OH\) cũng là đường phân giác, suy ra \(\widehat {DOC} = 2.\widehat {COH} = 2.30^\circ = 60^\circ \)
Do đó số đo cung nhỏ $CD$ là $60^\circ $ và số đo cung lớn $CD$ là $360^\circ - 60^\circ = 300^\circ $.
Hướng dẫn giải:
+) Sử dụng liên hệ giữa đường kính và dây
+) Số đo cung
- Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
- Số đo của cung lớn bằng hiệu giữa \({360^0}\) và số đo của cung nhỏ (có chung $2$ mút với cung lớn).
