Bài tập mạch xoay chiều RLC - pha u, i - viết u, i

Sử dụng giản đồ vec tơ ghép:

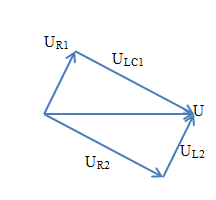
Vì I bằng nhau nên U_R1 = U_R2 vậy hình tạo thành là hình vuông

Ta có:

\(\left\{ \begin{array}{l}{Z_1} = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} \\{Z_2} = \sqrt {{R^2} + {Z_L}^2} \end{array} \right.\)

Vì đạt cùng điện áp hiệu dụng, mà giả thiết hai dòng điện có cùng giá trị hiệu dụng nên ta có:

\({Z_1} = {Z_2} \Leftrightarrow \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}}  = \sqrt {{R^2} + Z_L^2} \)

\( \Leftrightarrow {({Z_L} - {Z_C})^2} = Z_L^2 \Leftrightarrow \left| {{Z_L} - {Z_C}} \right| = {Z_L}\)

\( \Leftrightarrow {Z_C} = 2{{\rm{Z}}_L}\)

Theo bài ra, phương trình điện áp hai đầu đoạn mạch là:

\(u = {U_0}\cos \left( {\omega t + \varphi } \right)\left( V \right)\)

Độ lệch pha của dòng điện và điện áp trong mạch trong hai lần, lần lượt là:

\(\left\{ \begin{array}{l}\frac{{{Z_C} - {Z_L}}}{R} = \frac{\pi }{3} - \varphi \\\frac{{{Z_L}}}{R} = \varphi  - \left( { - \frac{\pi }{6}} \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\frac{{{Z_L}}}{R} = \frac{\pi }{3} - \varphi \\\frac{{{Z_L}}}{R} = \varphi  + \frac{\pi }{6}\end{array} \right.\)

\( \Rightarrow \frac{\pi }{3} - \varphi  = \varphi  + \frac{\pi }{6} \Leftrightarrow \varphi  = \frac{\pi }{{12}}\)

Mà U_R1 = U_L2 => \(R = {Z_L} = \left| {{Z_L} - {Z_C}} \right| \Rightarrow R = {Z_L} = \dfrac{1}{2}{Z_C}\)

Chuẩn hóa R = 1. Ta có :

\({I_{01}} = \dfrac{U}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }} = \dfrac{U}{{\sqrt {{1^2} + {{(2 - 1)}^2}} }} \Rightarrow I = \dfrac{U}{\sqrt 2} V\)

\({I_{03}} = \dfrac{U}{{{Z_C}}} = \dfrac{U}{2} = \sqrt 2 A\)

Mà i₃ chỉ có tụ và điện trở nên pha ban đầu của i₃ = 1,37 rad

Độ lệch pha giữa u và i:

\(\begin{array}{l}\tan \varphi  =  - \dfrac{{{Z_C}}}{R} =  - \dfrac{{100}}{{100}} =  - 1 \Rightarrow {\varphi _u} - {\varphi _i} =  - \dfrac{\pi }{4}\\ \Rightarrow {\varphi _i} = {\varphi _u} + \dfrac{\pi }{4} = \dfrac{\pi }{4}\end{array}\)

→ Phương trình của cường độ dòng điện: \(i = \sqrt 2 cos\left( {100\pi t + \dfrac{\pi }{4}} \right)A\)

Ta có:

+ Cảm kháng: \({Z_L} = \omega L = 100\pi .\dfrac{1}{\pi } = 100\Omega \)

+ Dung kháng: \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{2.10}^{ - 4}}}}{\pi }}} = 50\Omega \)

Tổng trở: \(Z = \left| {{Z_L} - {Z_C}} \right| = 50\Omega \)

Cường độ dòng điện cực đại trong mạch: \({I_0} = \dfrac{{{U_0}}}{Z} = \dfrac{{100\sqrt 2 }}{{50}} = 2\sqrt 2 A\)

Mạch chỉ có cuộn cảm thuần và tụ điện và có \({Z_L} > {Z_C} \Rightarrow \) điện áp nhanh pha \(\dfrac{\pi }{2}\) so với dòng điện

\( \Rightarrow {\varphi _i} = {\varphi _u} - \dfrac{\pi }{2} = \dfrac{\pi }{6} - \dfrac{\pi }{2} =  - \dfrac{\pi }{3}\)

\( \Rightarrow \) Cường độ dòng điện qua đoạn mạch: \(i = 2\sqrt 2 cos\left( {100\pi t - \dfrac{\pi }{3}} \right)\)

Áp dụng định luật Ôm cho đoạn mạch có dòng điện một chiều chạy qua:

\(I = \frac{U}{R} \Rightarrow R = \frac{U}{I} = \frac{{30}}{1} = {30_{}}\Omega \)

Áp dụng công thức tính điện trở đoạn mạch:

\(Z = \sqrt {{R^2} + {{\left( {\omega L} \right)}^2}} = \sqrt {{{30}^2} + {{\left( {\frac{1}{{4\pi }}.120\pi } \right)}^2}} = 30{\sqrt 2 _{}}\Omega \)

Áp dụng định luật Ôm cho đoạn mạch xoay chiều:

\(I = \frac{U}{Z} = \frac{{150}}{{30\sqrt 2 }} = \frac{5}{{\sqrt 2 }}A\)

Tính góc lệch giữa pha của điện áp và dòng điện:

\(\tan \varphi = \frac{{\omega L}}{R} = \frac{{30}}{{30}} = 1 \Rightarrow \varphi = {\varphi _u} - {\varphi _i} = \frac{\pi }{4} \Rightarrow {\varphi _i} = - \frac{\pi }{4}\)

Phương trình dòng điện:

\(i = \frac{5}{{\sqrt 2 }}.\sqrt 2 .\cos \left( {120\pi t - \frac{\pi }{4}} \right)V = 5.\cos \left( {120\pi t - \frac{\pi }{4}} \right)A\)

Áp dụng công thức định luật Ôm cho đoạn mạch xoay chiều chỉ gồm một phần tử ta có:

\(\left\{ \begin{gathered}
{I_L} = \frac{U}{{{Z_L}}} \Rightarrow {Z_L} = \frac{U}{{{I_L}}} \hfill \\
{I_C} = \frac{U}{{{Z_C}}} \Rightarrow {Z_C} = \frac{U}{{{I_C}}} \hfill \\
{I_R} = \frac{U}{R} \Rightarrow R = \frac{U}{{{I_R}}} \hfill \\
\end{gathered} \right.\)

Khi mắc cả 3 phần tử vào mạng điện xoay chiều nói trên:

\(\begin{gathered}
I = \frac{U}{Z} = \frac{U}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }} = \frac{U}{{\sqrt {{{\left( {\frac{U}{{{I_R}}}} \right)}^2} + {{\left( {\frac{U}{{{I_L}}} - \frac{U}{{{I_C}}}} \right)}^2}} }} \hfill \\
\Rightarrow I\, = \frac{U}{{\sqrt {{{\left( {\frac{U}{{0,25}}} \right)}^2} + {{\left( {\frac{U}{{0,5}} - \frac{U}{{0,2}}} \right)}^2}} }} = 0,2A \hfill \\
\end{gathered} \)

Ta có: \(\left\{ \begin{array}{l}R = 40\Omega \\{Z_L} = \omega L = 60\Omega \end{array} \right.\)

Công suất tiêu thụ trên đoạn mạch:

\(P = UIco{\rm{s}}\varphi  = \frac{{{U^2}}}{{{Z^2}}}R \Leftrightarrow 320 = \frac{{{{\left( {80\sqrt 2 } \right)}^2}}}{{{Z^2}}}40\)

\( \Rightarrow Z = 40\Omega  \Rightarrow {Z_L} = {Z_C} = 60\Omega  \Rightarrow {\varphi _u} = {\varphi _i}\)

\( \Rightarrow {I_0} = \frac{{{U_0}}}{Z} = \frac{{160}}{{40}} = 4A \Rightarrow {U_{0C}} = {I_0}{Z_C} = 4.60 = 240V\)

Lại có: \({\varphi _{{u_C}}} - {\varphi _i} =  - \frac{\pi }{2} \Rightarrow {\varphi _{{u_C}}} = {\varphi _i} - \frac{\pi }{2} = \frac{\pi }{6} - \frac{\pi }{2} =  - \frac{\pi }{3}\)

\( \Rightarrow {u_C} = 240co{\rm{s}}\left( {100\pi t - \frac{\pi }{3}} \right)V\)

R thay đổi để công suất cực đại, khi đó ta có: \(R = {Z_L}\) \( \Rightarrow {U_{0R}} = {U_{0L}}\)

Lại có: \(U_0^2 = U_{0R}^2 + U_{0L}^2 \Rightarrow {U_{0L}} = {U_{0R}} = \frac{{{U_0}}}{{\sqrt 2 }} = 40V\)

Độ lệch pha của u so với i: \(\tan \varphi  = \frac{{{Z_L}}}{R} = 1 \Rightarrow \varphi  = \frac{\pi }{4}\)

Độ lệch pha của \({u_R}\) và \(u\) là: \(\Delta \varphi  = \frac{\pi }{4} = {\varphi _{{u_u}}} - {\varphi _R}\)

\( \Rightarrow {\varphi _{{u_L}}} = {\varphi _u} - \frac{\pi }{4} = \frac{\pi }{6} - \frac{\pi }{4} =  - \frac{\pi }{{12}}\)

\( \Rightarrow \) Biểu thức điện áp giữa hai đầu điện trở: \({u_R} = 40cos\left( {100\pi t - \frac{\pi }{{12}}} \right)V\)

Từ dữ kiện bài cho ta có giản đồ vecto:

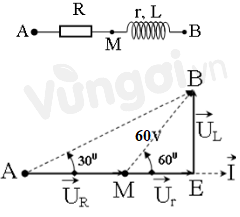
Từ hình vẽ ta có: \(\widehat {AMB} = {180^0} - \widehat {BME} = {120^0}\)

\( \Rightarrow \widehat {ABM} = {180^0} - \widehat {MAB} - \widehat {AMB} = {30^0}\)

\( \Rightarrow \Delta AMB\) cân tại M

\( \Rightarrow AM = MB = 60 \Leftrightarrow {U_R} = {U_d} = 60V\)

Áp dụng định lí hàm số cos trong tam giác AMB có:

\(\begin{array}{l}A{B^2} = A{M^2} + B{M^2} - 2.AM.BM.cos\widehat {AMB}\\ \Leftrightarrow {U^2} = U_R^2 + U_d^2 - 2.{U_R}{U_d}.cos\widehat {AMB}\\ \Leftrightarrow {U^2} = {60^2} + {60^2} - 2.60.60\cos 120 = 10800\\ \Rightarrow U = 60\sqrt 3 V\end{array}\)