Mạch điện xoay chiều gồm điện trở thuần \(R = 30\Omega \) mắc nối tiếp với cuộn dây. Đặt vào hai đầu mạch một hiệu điện thế xoay chiều \(u = U\sqrt 2 .cos\left( {100\pi t} \right)V\) thì hiệu điện thế hiệu dụng ở hai đầu cuộn dây là \({U_d} = 60V\) và dòng điện trong mạch lệch pha \(\dfrac{\pi }{6}\) so với u và lệch pha \(\dfrac{\pi }{3}\) so với \({u_d}\). Hiệu điện thế hiệu dụng ở hai đầu mạch U có giá trị
Trả lời bởi giáo viên
Từ dữ kiện bài cho ta có giản đồ vecto:
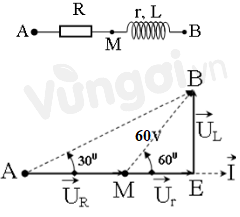
Từ hình vẽ ta có: \(\widehat {AMB} = {180^0} - \widehat {BME} = {120^0}\)
\( \Rightarrow \widehat {ABM} = {180^0} - \widehat {MAB} - \widehat {AMB} = {30^0}\)
\( \Rightarrow \Delta AMB\) cân tại M
\( \Rightarrow AM = MB = 60 \Leftrightarrow {U_R} = {U_d} = 60V\)
Áp dụng định lí hàm số cos trong tam giác AMB có:
\(\begin{array}{l}A{B^2} = A{M^2} + B{M^2} - 2.AM.BM.cos\widehat {AMB}\\ \Leftrightarrow {U^2} = U_R^2 + U_d^2 - 2.{U_R}{U_d}.cos\widehat {AMB}\\ \Leftrightarrow {U^2} = {60^2} + {60^2} - 2.60.60\cos 120 = 10800\\ \Rightarrow U = 60\sqrt 3 V\end{array}\)
Hướng dẫn giải:
Vẽ giản đồ vecto.
Sử dụng định lí hàm số cos: \({c^2} = {a^2} + {b^2} - 2.ab.cosC\)