Trên mặt phẳng tọa độ \(Oxy\), xác định vị trí tương đối của điểm \(A\left( { - 3; - 4} \right)\) và đường tròn tâm là gốc tọa độ \(O\), bán kính \(R = 3\).
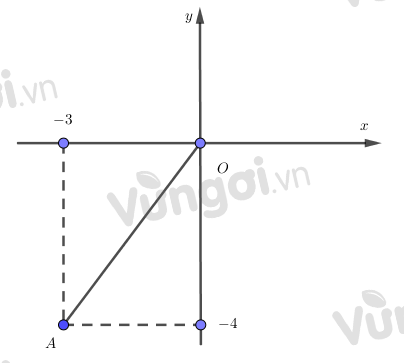
Ta có: \(O{A^2} = {\left| {{x_A}} \right|^2} + {\left| {{y_A}} \right|^2}\) (Định lý Py-ta-go)
\( \Rightarrow OA = \sqrt {{{\left| {{x_a}} \right|}^2} + {{\left| {{y_A}} \right|}^2}} = \sqrt {{3^3} + {4^2}} = 5 > 3 = R\)
Do đó \(A\) nằm bên ngoài đường tròn tâm \(O\) bán kính \(R = 3cm.\)
Tính bán kính đường tròn đi qua bốn điểm \(A,N,G,M\) với \(G\) là giao của \(BM\) và \(CN\)
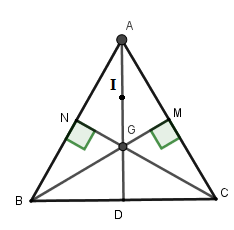
Vì \(G\) là giao điểm của hai đường cao\(BM,CN\) nên \(G\) là trực tâm \(\Delta ABC\)
Ta có \(G\) là trực tâm \(\Delta ABC\) nên \(G\) cũng là trọng tâm \(\Delta ABC\) suy ra \(AG = \dfrac{2}{3}AD\).
\(D\) là trung điểm \(BC \Rightarrow AD \bot BD\); \(DC = \dfrac{{BC}}{2} = \dfrac{3}{2}\)
Theo định lý Pytago cho tam giác vuông \(ADC\) ta có \(AD = \sqrt {B{C^2} - D{C^2}} = \dfrac{{3\sqrt 3 }}{2}\)\( \Rightarrow AG = \dfrac{2}{3}.\dfrac{{3\sqrt 3 }}{2} = \sqrt 3 \)
Gọi \(I\) là trung điểm của \(AG\). Xét tam giác vuông \(ANG\) có \(IN = IA = IG\), xét tam giác vuông \(AMG\) có \(IM = IA = IG\) nên \(IM = IN = IA = IG = \dfrac{{AG}}{2}\)
Hay 4 điểm \(A,N,G,M\) cùng thuộc một đường tròn bán kính \(R = \dfrac{{AG}}{2} = \dfrac{{\sqrt 3 }}{2}\)
Bốn điểm nào sau đây cùng thuộc một đường tròn?
Bốn điểm nào sau đây cùng thuộc một đường tròn?

Cho tam giác \(ABC\) vuông tại \(A\) , có\(AB = 5cm;AC = 12cm\) . Tính bán kính đường tròn ngoại tiếp tam giác \(ABC\) .
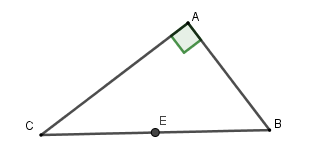
Vì tam giác \(ABC\) vuông tại\(A\) nên tâm đường tròn ngoại tiếp là trung điểm cạnh huyền \(BC\), bán kính là \(R = \dfrac{{BC}}{2}\).
Theo định lý Pytago ta có \(BC = \sqrt {A{C^2} + A{B^2}} = 13\) nên bán kính \(R = \dfrac{{13}}{2}\).
Cho hình chữ nhật \(ABCD\) có \(AB = 8cm,BC = 6cm\) .Tính bán kính đường tròn đi qua bốn đỉnh \(A,B,C,D\).
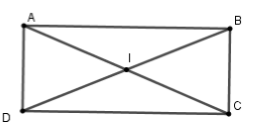
Gọi \(I\) là giao hai đường chéo, ta có \(IA = IB = IC = ID\) (vì \(BD = AC\) và \(I\) là trung điểm mỗi đường)
Nên bốn điểm \(A,B,C,D\) cùng thuộc đường tròn tâm \(I\) bán kính \(R = \dfrac{{AC}}{2}\)
Theo định lý Pytago trong tam giác vuông \(ABC\) ta có \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{8^2} + {6^2}} = 10\) nên \(R = \dfrac{{AC}}{2} = \dfrac{{10}}{2} = 5\,cm\)
Vậy bán kính cần tìm là \(R = 5\,cm\).
Số tâm đối xứng của đường tròn là:
Đường tròn là hình có tâm đối xứng. Tâm đường tròn là tâm đối xứng của đường tròn đó.
Nên đường tròn có một tâm đối xứng duy nhất là tâm của đường tròn.
Khẳng định nào sau đây là đúng khi nói về trục đối xứng của đường tròn
Đường tròn là hình có trục đối xứng. Bất kỳ đường kính nào cũng là trục đối xứng của đường tròn
Nên đường tròn có vô số trục đối xứng.
Tâm đường tròn ngoại tiếp tam giác là
Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó.
Cho đường tròn $\left( {O;R} \right)$ và điểm $M$ bất kỳ, biết rằng $OM = R$. Chọn khẳng định đúng?
Cho điểm $M$ và đường tròn $\left( {O;R} \right)$ ta so sánh khoảng cách $OM$ với bán kính $R$ để xác định vị trí tương đối theo bảng sau:
|
Vị trí tương đối |
Hệ thức |
|
M nằm trên đường tròn $\left( O \right)$ |
\(OM = R\) |
|
M nằm trong đường tròn $\left( O \right)$ |
\(OM < R\) |
|
M nằm ngoài đường tròn $\left( O \right)$ |
\(OM > R\) |
Xác định tâm và bán kính của đường tròn đi qua cả bốn đỉnh của hình vuông $ABCD$ cạnh $a.$
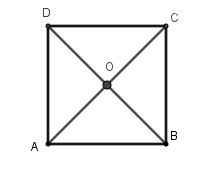
Gọi $O$ là giao hai đường chéo của hình vuông $ABCD$. Khi đó theo tình chất của hình vuông ta có $OA = OB = OC = OD$ nên $O$ là tâm đường tròn ngoại tiếp hình vuông $ABCD$, bán kính $R = OA = \dfrac{{AC}}{2}$
Xét tam giác $ABC$ vuông cân tại $B$ ta có $A{C^2} = A{B^2} + B{C^2} \Rightarrow AC = a\sqrt 2 $$ \Rightarrow R = \dfrac{{a\sqrt 2 }}{2}$
Vậy tâm đường tròn ngoại tiếp hình vuông $ABCD$ cạnh $a$ là giao điểm hai đường chéo, bán kính là $R = \dfrac{{a\sqrt 2 }}{2}$.
Tâm của đường tròn ngoại tiếp tam giác vuông là
Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp.
Cho tam giác $ABC$ có các đường cao $BD,CE$ . Biết rằng bốn điểm $B,E,D,C$ cùng nằm trên một đường tròn. Chỉ rõ tâm và bán kính của đường tròn đó.
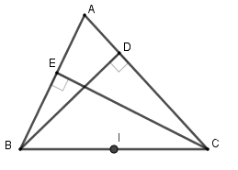
Gọi $I$ là trung điểm của $BC$.
Xét tam giác $BEC$ vuông tại $E$ có $EI = IB = IC = \dfrac{{BC}}{2}$ (vì $EI$ là đường trung tuyến ứng với cạnh huyền)
Xét tam giác $BDC$ vuông tại $D$ có $DI = IB = IC = \dfrac{{BC}}{2}$ (vì $DI$ là đường trung tuyến ứng với cạnh huyền)
Từ đó ta có $ID = IE = IB = IC = \dfrac{{BC}}{2}$ nên $I$ là tâm đường tròn ngoại tiếp tứ giác $DEBC$ và bán kính $R = \dfrac{{BC}}{2}$.
Trên mặt phẳng tọa độ $Oxy$, xác định vị trí tương đối của điểm $A\left( { - 1; - 1} \right)$ và đường tròn tâm là gốc tọa độ $O$, bán kính $R = 2\,$.
Ta có $OA = \sqrt {{{\left( { - 1 - 0} \right)}^2} + {{\left( { - 1 - 0} \right)}^2}} = \sqrt 2 < 2 = R$ nên $A$ nằm trong đường tròn tâm $O$ bán kính $R = 2$.
Cho tam giác $ABC$ vuông tại $A$ , có$AB = 15cm;AC = 20cm$. Tính bán kính đường tròn ngoại tiếp tam giác $ABC.$
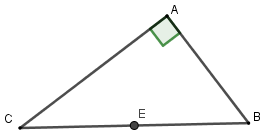
Vì tam giác $ABC$ vuông tại$A$ nên tâm đường tròn ngoại tiếp là trung điểm cạnh huyền $BC$, bán kính là $R = \dfrac{{BC}}{2}$.
Theo định lý Pytago ta có $BC = \sqrt {A{C^2} + A{B^2}} = 25$ nên bán kính $R = \dfrac{{25}}{2}$.
Cho hình chữ nhật $ABCD$ có$AB = 12cm,BC = 5cm$ .Tính bán kính đường tròn đi qua bốn đỉnh $A,B,C,D$.
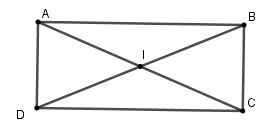
Gọi $I$ là giao hai đường chéo, ta có $IA = IB = IC = ID$ (vì $BD = AC$ và $I$ là trung điểm mỗi đường)
Nên bốn điểm $A,B,C,D$ cùng thuộc đường tròn tâm $I$ bán kính $R = \dfrac{{AC}}{2}$
Theo định lý Pytago trong tam giác vuông $ABC$ ta có $AC = \sqrt {A{B^2} + B{C^2}} = 13$ nên $R = \dfrac{{AC}}{2} = 6,5\,cm$
Vậy bán kính cần tìm là $R = 6,5\,cm$.
Cho hình vuông $ABCD$. Gọi $M,N$ lần lượt là trung điểm của $AB,BC$ . Gọi $E$ là giao điểm của $CM$ và $DN$. Tâm của đường tròn đi qua bốn điểm $A,D,E,M$ là
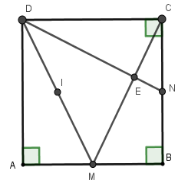
+) Ta có \(\Delta DCN = \Delta CMB\left( {c - g - c} \right) \)
$\Rightarrow\widehat {CDN} = \widehat {ECN}$ nên $\widehat {CNE} + \widehat {ECN} = \widehat {CNE} + \widehat {CDN} = 90^\circ $ suy ra $\widehat {CEN} = 90^\circ \Rightarrow CM \bot DN$
+) Gọi $I$ là trung điểm của $DM$.
Xét tam giác vuông $ADM$ ta có $AI = ID = IM = \dfrac{{DM}}{2}$. Xét tam giác vuông $DEM$ ta có $EI = ID = IM = \dfrac{{DM}}{2}$
Nên $EI = ID = IM = IA = \dfrac{{DM}}{2}$
Do đó bốn điểm $A,D,E,M$ cùng thuộc đường tròn tâm $I$ bán kính $\dfrac{{DM}}{2}$.
Cho tam giác $ABC$ cân tại $A$ , đường cao $AH = 2cm,BC = 8cm$ . Đường vuông góc với $AC$ tại $C$ cắt đường thẳng $AH$ ở $D$ .
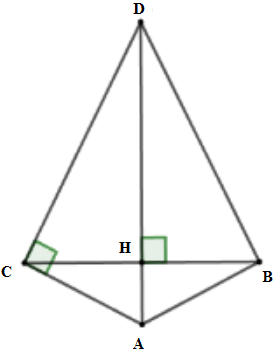
Các điểm nào sau đây cùng thuộc một đường tròn?
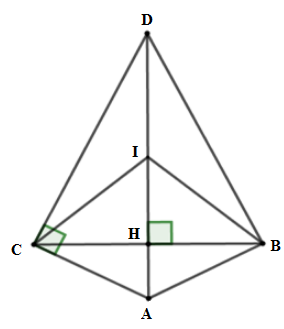
Ta có $\Delta ABC$ cân tại $A$ có đường cao $AH$ nên $AH$ cũng là đường phân giác $ \Rightarrow \widehat {CAD} = \widehat {DAB}$
Suy ra $\Delta ACD = \Delta ABD\left( {c - g - c} \right)$ nên $\widehat {ABD} = \widehat {ACD} = 90^\circ $.
Lấy $I$ là trung điểm $AD$. Xét hai tam giác vuông $ABD$ và $ACD$ có $IA = ID = IB = IC = \dfrac{{AD}}{2}$
Nên $I$ là điểm cách đều $A,B,D,C$ hay $A,B,D,C$ cùng nằm trên dường tròn tâm $I$ đường kính $AD$.
Cho tam giác $ABC$ cân tại $A$ , đường cao $AH = 2cm,BC = 8cm$ . Đường vuông góc với $AC$ tại $C$ cắt đường thẳng $AH$ ở $D$ .

Tính đường kính của đường tròn đi qua các điểm $A, B, D, C.$
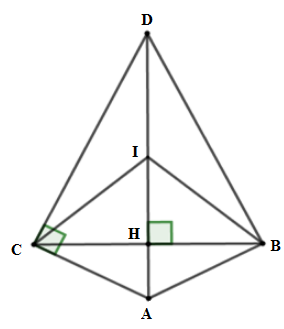
Từ câu trước ta có bốn điểm $A,B,D,C$ cùng thuộc đường tròn đường kính $AD$ suy ra ta cần tính độ dài $AD$.
Vì $BC = 8\,cm \Rightarrow BH = 4\,cm$. Áp dụng định lý Pytago cho tam giác vuông $AHB$ ta được $AB = \sqrt {A{H^2} + B{H^2}} = \sqrt {4 + 16} = 2\sqrt 5 $
Áp dụng hệ thức lượng trong tam giác vuông $ABD$ ta có $A{B^2} = AH.AD$$\Rightarrow AD = \dfrac{{A{B^2}}}{{AH}} = \dfrac{{20}}{2} = 10$
Vậy đường kính cần tìm là $10\,cm$.
Cho tam giác đều $ABC$ cạnh bằng $a$ , các đường cao là $BM$ và $CN$ . Gọi $D$ là trung điểm cạnh $BC$ .
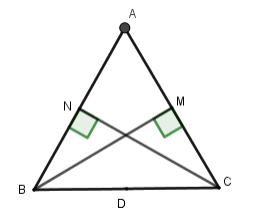
Đường tròn đi qua bốn điểm $B,N,M,C$ là
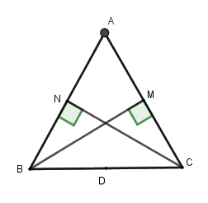
Gọi $D$ là trung điểm $BC$.
Xét hai tam giác vuông $BNC$ và $BMC$ có $ND,MD$ là hai đường trung tuyến
$ \Rightarrow DN = DB = DC = DM = \dfrac{{BC}}{2}$ nên bốn điểm $B,N,M,C$ cùng thuộc đường tròn tâm $D$ bán kính $\dfrac{{BC}}{2}$.

