Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) vuông tại \(A\) , có\(AB = 5cm;AC = 12cm\) . Tính bán kính đường tròn ngoại tiếp tam giác \(ABC\) .
Trả lời bởi giáo viên
Đáp án đúng: c
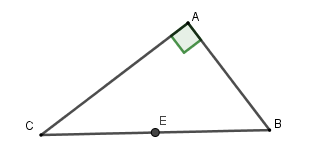
Vì tam giác \(ABC\) vuông tại\(A\) nên tâm đường tròn ngoại tiếp là trung điểm cạnh huyền \(BC\), bán kính là \(R = \dfrac{{BC}}{2}\).
Theo định lý Pytago ta có \(BC = \sqrt {A{C^2} + A{B^2}} = 13\) nên bán kính \(R = \dfrac{{13}}{2}\).
Hướng dẫn giải:
Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp.
Sử dụng định lý Pytago để tính toán
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
