Cho hình vuông \(ABCD\) cạnh \(4cm.\) Gọi \(M,N\) lần lượt là trung điểm của \(AB,BC.\) Gọi \(E\) là giao điểm của \(CM\) và \(DN.\) Bán kính của đường tròn đi qua bốn điểm \(A,D,E,M\) là
Trả lời bởi giáo viên
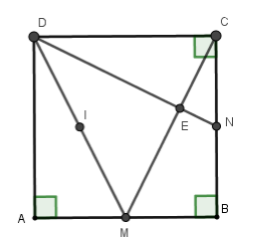
+) Ta có \(\widehat {CDN} = \widehat {ECN}\) (vì cùng phụ với \(\widehat {CNE}\)) nên \(\widehat {CNE} + \widehat {ECN} = \widehat {CNE} + \widehat {CDN} = 90^\circ \) suy ra \(\widehat {CEN} = 90^\circ \Rightarrow CM \bot DN\)
+) Gọi \(I\) là trung điểm của \(DM\).
Xét tam giác vuông \(ADM\) ta có \(AI = ID = IM = \dfrac{{DM}}{2}\). Xét tam giác vuông \(DEM\) ta có \(EI = ID = IM = \dfrac{{DM}}{2}\)
Nên \(EI = ID = IM = IA = \dfrac{{DM}}{2}\)
Do đó bốn điểm \(A,D,E,M\) cùng thuộc đường tròn tâm \(I\) bán kính \(R = \dfrac{{DM}}{2}\).
Xét tam giác \(ADM\) vuông tại \(A\) có \(AD = 4cm;AM = \dfrac{{AB}}{2} = 2cm\) nên theo định lý Pytago ta có \(DM = \sqrt {A{D^2} + A{M^2}} = \sqrt {{4^2} + {2^2}} = 2\sqrt 5 \)
Suy ra bán kính đường tròn đi qua 4 điểm \(A,D,E,M\) là \(R = \dfrac{{DM}}{2} = \dfrac{{2\sqrt 5 }}{2} = \sqrt 5 cm\)
Hướng dẫn giải:
Bước 1: Đưa các điểm đã cho về các đỉnh của tam giác vuông.
Bước 2: Tìm điểm cách đều cả bốn đỉnh \(A,D,E,M\). Điểm đó chính là tâm của đường tròn.
Bước 3: Tính bán kính đường tròn
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
