Câu hỏi:
2 năm trước
Trên mặt phẳng tọa độ \(Oxy\), xác định vị trí tương đối của điểm \(A\left( { - 3; - 4} \right)\) và đường tròn tâm là gốc tọa độ \(O\), bán kính \(R = 3\).
Trả lời bởi giáo viên
Đáp án đúng: a
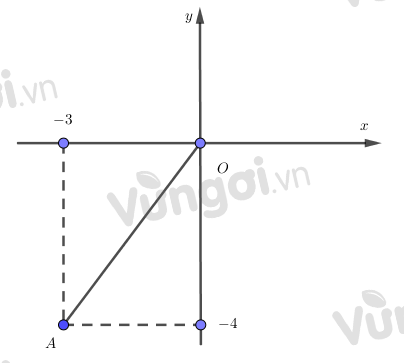
Ta có: \(O{A^2} = {\left| {{x_A}} \right|^2} + {\left| {{y_A}} \right|^2}\) (Định lý Py-ta-go)
\( \Rightarrow OA = \sqrt {{{\left| {{x_a}} \right|}^2} + {{\left| {{y_A}} \right|}^2}} = \sqrt {{3^3} + {4^2}} = 5 > 3 = R\)
Do đó \(A\) nằm bên ngoài đường tròn tâm \(O\) bán kính \(R = 3cm.\)
Hướng dẫn giải:
+ Sử dụng định lý Py-ta-go để tính OA
+ Sử dụng vị trí tương đối giữa điểm và đường tròn
Cho điểm \(M\) và đường tròn \(\left( {O;R} \right)\) ta so sánh khoảng cách \(OM\) với bán kính R để xác định vị trí tương đối theo bảng sau:


