Câu hỏi:
2 năm trước
Xác định tâm và bán kính của đường tròn đi qua cả bốn đỉnh của hình vuông $ABCD$ cạnh $a.$
Trả lời bởi giáo viên
Đáp án đúng: c
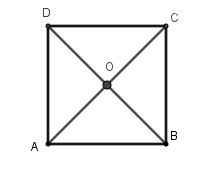
Gọi $O$ là giao hai đường chéo của hình vuông $ABCD$. Khi đó theo tình chất của hình vuông ta có $OA = OB = OC = OD$ nên $O$ là tâm đường tròn ngoại tiếp hình vuông $ABCD$, bán kính $R = OA = \dfrac{{AC}}{2}$
Xét tam giác $ABC$ vuông cân tại $B$ ta có $A{C^2} = A{B^2} + B{C^2} \Rightarrow AC = a\sqrt 2 $$ \Rightarrow R = \dfrac{{a\sqrt 2 }}{2}$
Vậy tâm đường tròn ngoại tiếp hình vuông $ABCD$ cạnh $a$ là giao điểm hai đường chéo, bán kính là $R = \dfrac{{a\sqrt 2 }}{2}$.
Hướng dẫn giải:
Xác định điểm cách đều cả bốn đỉnh của hình vuông. Điểm đó chính là tâm của đường tròn ngoại tiếp hình vuông.
Câu hỏi khác
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
