Câu hỏi:
2 năm trước
Cho hình vuông $ABCD$. Gọi $M,N$ lần lượt là trung điểm của $AB,BC$ . Gọi $E$ là giao điểm của $CM$ và $DN$. Tâm của đường tròn đi qua bốn điểm $A,D,E,M$ là
Trả lời bởi giáo viên
Đáp án đúng: a
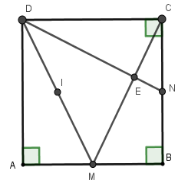
+) Ta có \(\Delta DCN = \Delta CMB\left( {c - g - c} \right) \)
$\Rightarrow\widehat {CDN} = \widehat {ECN}$ nên $\widehat {CNE} + \widehat {ECN} = \widehat {CNE} + \widehat {CDN} = 90^\circ $ suy ra $\widehat {CEN} = 90^\circ \Rightarrow CM \bot DN$
+) Gọi $I$ là trung điểm của $DM$.
Xét tam giác vuông $ADM$ ta có $AI = ID = IM = \dfrac{{DM}}{2}$. Xét tam giác vuông $DEM$ ta có $EI = ID = IM = \dfrac{{DM}}{2}$
Nên $EI = ID = IM = IA = \dfrac{{DM}}{2}$
Do đó bốn điểm $A,D,E,M$ cùng thuộc đường tròn tâm $I$ bán kính $\dfrac{{DM}}{2}$.
Hướng dẫn giải:
Bước 1: Đưa các điểm đã cho về các đỉnh của tam giác vuông.
Bước 2: Tìm điểm cách đều cả bốn đỉnh $A,D,E,M$. Điểm đó chính là tâm của đường tròn.
Câu hỏi khác
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
