Câu hỏi:
3 năm trước
Cho tam giác đều $ABC$ cạnh bằng $a$ , các đường cao là $BM$ và $CN$ . Gọi $D$ là trung điểm cạnh $BC$ .
Đường tròn đi qua bốn điểm $B,N,M,C$ là
Trả lời bởi giáo viên
Đáp án đúng: a
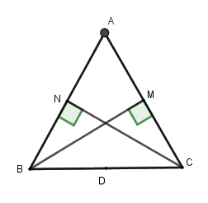
Gọi $D$ là trung điểm $BC$.
Xét hai tam giác vuông $BNC$ và $BMC$ có $ND,MD$ là hai đường trung tuyến
$ \Rightarrow DN = DB = DC = DM = \dfrac{{BC}}{2}$ nên bốn điểm $B,N,M,C$ cùng thuộc đường tròn tâm $D$ bán kính $\dfrac{{BC}}{2}$.
Hướng dẫn giải:
Xác định điểm cách đều cả bốn đỉnh cho trước. Điểm đó chính là tâm của đường tròn.

