Câu hỏi:
3 năm trước
Cho hình chữ nhật $ABCD$ có$AB = 12cm,BC = 5cm$ .Tính bán kính đường tròn đi qua bốn đỉnh $A,B,C,D$.
Trả lời bởi giáo viên
Đáp án đúng: d
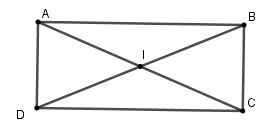
Gọi $I$ là giao hai đường chéo, ta có $IA = IB = IC = ID$ (vì $BD = AC$ và $I$ là trung điểm mỗi đường)
Nên bốn điểm $A,B,C,D$ cùng thuộc đường tròn tâm $I$ bán kính $R = \dfrac{{AC}}{2}$
Theo định lý Pytago trong tam giác vuông $ABC$ ta có $AC = \sqrt {A{B^2} + B{C^2}} = 13$ nên $R = \dfrac{{AC}}{2} = 6,5\,cm$
Vậy bán kính cần tìm là $R = 6,5\,cm$.
Hướng dẫn giải:
Tìm điểm cách đều cả bốn đỉnh của hình chữ nhật, điểm đó chính là tâm đường tròn. Bán kính là khoảng cách từ tâm đến một điểm bất kỳ trên đường tròn.

