Câu hỏi:
2 năm trước
Cho hình chữ nhật \(ABCD\) có \(AB = 8cm,BC = 6cm\) .Tính bán kính đường tròn đi qua bốn đỉnh \(A,B,C,D\).
Trả lời bởi giáo viên
Đáp án đúng: a
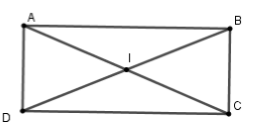
Gọi \(I\) là giao hai đường chéo, ta có \(IA = IB = IC = ID\) (vì \(BD = AC\) và \(I\) là trung điểm mỗi đường)
Nên bốn điểm \(A,B,C,D\) cùng thuộc đường tròn tâm \(I\) bán kính \(R = \dfrac{{AC}}{2}\)
Theo định lý Pytago trong tam giác vuông \(ABC\) ta có \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{8^2} + {6^2}} = 10\) nên \(R = \dfrac{{AC}}{2} = \dfrac{{10}}{2} = 5\,cm\)
Vậy bán kính cần tìm là \(R = 5\,cm\).
Hướng dẫn giải:
Tìm điểm cách đều cả bốn đỉnh của hình chữ nhật, điểm đố chính à tâm đường tròn. Bán kính là khoảng cách từ tâm đến một điểm bất kỳ trên đường tròn.
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
