Khi mắc cuộn cảm có độ tự cảm L1 với tụ điện có điện dung C thì tần số dao động của mạch là f1, khi mắc cuộn cảm có độ tự cảm L2 với tụ điện có điện dung C thì tần số dao động của mạch là f2. Nhận định nào sau đây là đúng:
Ta có:
Mạch gồm L1 và C có tần số f1 - Mạch gồm L2 và C có tần số f2
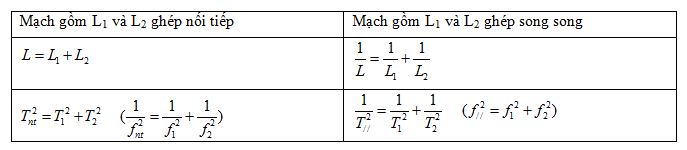
Khi mắc cuộn cảm có độ tự cảm L1 với tụ điện có điện dung C thì tần số dao động của mạch là f1 = 3 kHz, khi mắc cuộn cảm có độ tự cảm L2 với tụ điện có điện dung C thì tần số dao động của mạch là f2= 4 kHz. Tần số dao động của mạch khi mắc L1 nối tiếp với L2 và tần số dao động của mạch khi mắc L1 song song L2 là:
Ta có:
- Khi mắc cuộn cảm có độ tự cảm L1 thì tần số dao động của mạch là f1
- Khi mắc cuộn cảm có độ tự cảm L2 thì tần số dao động của mạch là f2
- Khi mắc nối tiếp L1 và L2 thì tần số dao động của mạch là:
$\frac{1}{{f_{nt}^2}} = \frac{1}{{f_1^2}} + \frac{1}{{f_2^2}} = \frac{{f_1^2 + f_2^2}}{{f_1^2f_2^2}} \to {f_{nt}} = \frac{{{f_1}{f_2}}}{{\sqrt {f_1^2 + f_2^2} }} = \frac{{{{3.10}^3}{{.4.10}^3}}}{{\sqrt {{{({{3.10}^3})}^2} + {{({{4.10}^3})}^2}} }} = 2,{4.10^3}H{\text{z}} = 2,4kH{\text{z}}$
- Khi mắc song song L1 và L2 thì tần số dao động của mạch là:
$f_{//}^2 = f_1^2 + f_2^2 \to {f_{//}} = \sqrt {f_1^2 + f_2^2} = \sqrt {{{({{3.10}^3})}^2} + {{\left( {{{4.10}^3}} \right)}^2}} = {5.10^3}H{\text{z}} = 5kH{\text{z}}$
Một tụ điện có điện dung C được nạp điện tới điện tích q. Khi nối tụ với cuộn cảm thuần có độ tự cảm L1 thì trong mạch có dao động điện từ riêng với cường độ dòng điện cực đại bằng 70mA. Khi nối tụ với cuộn cảm thuần có độ tự cảm L2 thì trong mạch có dao động điện từ riêng với cường độ dòng điện cực dại bằng 35mA. Nếu nối tụ với cuộn cảm thuần có độ tự cảm ${L_3} = 13{L_1} + 9{L_2}$ thì trong mạch có cường độ dòng điện cực đại bằng
Cách 1 :
Ta có:
\(\begin{array}{l}{I_1} = {\omega _1}q = \frac{q}{{\sqrt {{L_1}C} }} = > {L_1} = \frac{{{q^2}}}{{{I_1}^2C}}\\{I_2} = {\omega _2}q = \frac{q}{{\sqrt {{L_2}C} }} = > {L_2} = \frac{{{q^2}}}{{{I_2}^2C}}\end{array}\)
=> Khi sử dụng cuộn cảm có độ tự cảm \({L_3} = 13{L_1} + 9{L_2}\) thì cường độ dòng điện cực đại là :
\({I_3} = \frac{q}{{\sqrt {{L_3}C} }} = \frac{q}{{\sqrt {(13\frac{{{q^2}}}{{{I_1}^2C}} + 9\frac{{{q^2}}}{{{I_2}^2C}})C} }} = \frac{{{I_1}{I_2}}}{{\sqrt {13{I_2}^2 + 9{I_1}^2} }} = 10mA\)
Cách 2:
Ta có:
\(\begin{array}{l}{I_1} = {\omega _1}q = \frac{q}{{\sqrt {{L_1}C} }};{I_2} = {\omega _2}q = \frac{q}{{\sqrt {{L_2}C} }}\\ \to \frac{{{I_1}}}{{{I_2}}} = \sqrt {\frac{{{L_2}}}{{{L_1}}}} = \frac{{70}}{{35}} \to \frac{{{L_2}}}{{{L_1}}} = 4\\ \to {L_2} = 4{L_1}\end{array}\)
\(\begin{array}{l}{I_3} = \frac{q}{{\sqrt {{L_3}C} }} \to \frac{{{I_3}}}{{{I_1}}} = \sqrt {\frac{{{L_1}}}{{{L_3}}}} = \sqrt {\frac{{{L_1}}}{{13{L_1} + 9{L_2}}}} = \sqrt {\frac{{{L_1}}}{{13{L_1} + 9.4{L_1}}}} = \frac{1}{7}\\ \to {I_3} = \frac{{{I_1}}}{7} = \frac{{70}}{7} = 10mA\end{array}\)
Gọi A và vM lần lượt là biên độ và vận tốc cực đại của một chất điểm dao động điều hòa; Q0 và I0 lần lượt là điện tích cực đại trên một bản tụ điện và cường độ dòng điện cực đại trong mạch dao động LC đang hoạt động. Biểu thức \(\frac{{{v_M}}}{A}\) có cùng đơn vị với biểu thức
Ta có: \(\left\{ \begin{array}{l}\dfrac{{{v_M}}}{A}\left[ {\dfrac{{m/s}}{m} = \dfrac{1}{s}} \right]\\\dfrac{{{I_0}}}{{{Q_0}}}\left[ {\dfrac{A}{{A.s}} = \dfrac{1}{s}} \right]\end{array} \right.\)
Một mạch dao động điện từ lí tưởng gồm cuộn cảm thuần và tụ điện có điện dung thay đổi được. Khi điện dung của tụ điện có giá trị \(20 pF\) thì chu kì dao động riêng của mạch dao động là \(2,0 µs\). Khi điện dung của tụ điện có giá trị \(80 pF\) thì chu kì dao động riêng của mạch dao động là
Ta có chu kì của dao động mạch dao động điện từ LC:\(T = 2\pi \sqrt {LC} \)
\(\dfrac{{{T_1}}}{{{T_2}}} = \sqrt {\dfrac{{{C_1}}}{{{C_2}}}} \Leftrightarrow \dfrac{2}{{{T_2}}} = \sqrt {\dfrac{{20}}{{80}}} \)
\( \Leftrightarrow \dfrac{2}{{{T_2}}} = \dfrac{1}{2} \Leftrightarrow {T_2} = 4\mu s\)
Hai mạch dao động điện từ lí tưởng đang có dao động điện từ tự do với cùng cường độ dòng điện cực đại I0. Chu kì dao động riêng của mạch thứ nhất là T1, của mạch thứ hai là T2 = 2T1. Khi cường độ dòng điện trong hai mạch có cùng độ lớn và nhỏ hơn I0 thì độ lớn điện tích trên một bản tụ điện của mạch dao động thứ nhất là q1 và của mạch dao động thứ hai là q2. Tỉ số \(\dfrac{{{q_1}}}{{{q_2}}}\) là
Theo đề bài ta có: \({T_2} = 2{T_1} \Rightarrow {Q_{02}} = 2{Q_{01}}\)
Áp dụng công thức độc lập với thời gian cho hai mạch, ta có:
\(\left\{ \begin{array}{l}\dfrac{{{i^2}}}{{{I_0}^2}} + \dfrac{{{q_1}^2}}{{{Q_{01}}^2}} = 1\\\dfrac{{{i^2}}}{{{I_0}^2}} + \dfrac{{{q_2}^2}}{{{Q_{02}}^2}} = 1\end{array} \right. \Rightarrow \dfrac{{{q_1}^2}}{{{Q_{01}}^2}} = \dfrac{{{q_2}^2}}{{{Q_{02}}^2}} \Rightarrow \dfrac{{{q_1}}}{{{q_2}}} = \dfrac{{{Q_{01}}}}{{{Q_{02}}}} = 0,5\)
Một mạch dao động điện từ lí tưởng gồm cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C. Mạch dao động tự do với tần số là
Tần số dao động mạch LC: \(f = \frac{1}{{2\pi \sqrt {LC} }}\)
Đề thi thử THPT chuyên Lam Sơn - 2021
Một mạch dao động lí tưởng gồm cuộn dây thuần cảm có độ tự cảm L không đổi và tụ điện có điện dung C thay đổi được. Khi điện dung của tụ là \({C_1}\) thì chu kì dao động của mạch là \({3.10^{ - 8}}s\). Từ giá trị \({C_1}\) nếu điều chỉnh tăng thêm điện dung của tụ một lượng \(\Delta C\) thì chu kì dao động riêng của mạch là \({6.10^{ - 8}}s\). Từ giá trị \({C_1}\) nếu điều chỉnh tăng thêm điện dung của tụ một lượng \(9\Delta {C_1}\) thì chu kì dao động riêng của mạch là
+ Khi \(C = {C_1}\) có: \({T_1} = 2\pi \sqrt {L{C_1}} = {3.10^{ - 8}}s\)
+ Khi \(C = {C_1} + \Delta C\)có: \({T_2} = 2\pi \sqrt {L\left( {{C_1} + \Delta C} \right)} = {6.10^{ - 8}}s\)
\( \Rightarrow \frac{{{T_1}}}{{{T_2}}} = \sqrt {\frac{{{C_1}}}{{{C_1} + \Delta C}}} \Leftrightarrow \frac{3}{6} = \sqrt {\frac{{{C_1}}}{{{C_1} + \Delta C}}} \Rightarrow \Delta C = 3{C_1}\)
+ Khi \(C = {C_1} + 9\Delta C\)có: \(T = 2\pi \sqrt {L\left( {{C_1} + 9\Delta C} \right)} \)
\( \Rightarrow T = 2\pi \sqrt {L\left( {{C_1} + 9.3{C_1}} \right)} = 2\pi \sqrt {28L{C_1}} = 2\sqrt 7 {T_1} = 15,{87.10^{ - 3}}s\)
Một mạch dao động điện từ LC gồm cuộn dây thuần cảm có độ tự cảm L không đổi và tụ điện có C thay đổi được.Biết điện trở của dây dẫn là không đáng kể và trong mạch có dao động điện từ riêng. Khi điện dung có giá trị C1 thì tần số dao động riêng của mạch là f1. Khi điện dung có giá trị \({C_2} = 4{C_1}\) thì tần số dao động điện từ riêng trong mạch là
Ta có:
\(\left\{ \begin{array}{l}{f_1} = \frac{1}{{2\pi \sqrt {L{C_1}} }}\\{f_2} = \frac{1}{{2\pi \sqrt {L4{C_1}} }}\end{array} \right. \Leftrightarrow \frac{{{f_1}}}{{{f_2}}} = \frac{{2\pi \sqrt {L4{C_1}} }}{{2\pi \sqrt {L{C_1}} }} = 2\)
\( \Rightarrow {f_2} = \frac{{{f_1}}}{2}\)

