Có bao nhiêu giá trị của $n$ thỏa mãn hệ thức sau: \(\dfrac{{{P_n} - {P_{n - 1}}}}{{{P_{n + 1}}}} = \dfrac{1}{6}\)?
ĐK: \(n \ge 1\)
\(\begin{array}{l}\dfrac{{{P_n} - {P_{n - 1}}}}{{{P_{n + 1}}}} = \dfrac{1}{6} \Leftrightarrow \dfrac{{1.2.3...\left( {n - 1} \right)n - 1.2....\left( {n - 1} \right)}}{{1.2....\left( {n - 1} \right)n\left( {n + 1} \right)}} = \dfrac{1}{6}\\ \Leftrightarrow \dfrac{{1.2.3...\left( {n - 1} \right)\left( {n - 1} \right)}}{{1.2.3...\left( {n - 1} \right)n\left( {n + 1} \right)}} = \dfrac{1}{6}\\ \Leftrightarrow \dfrac{{n - 1}}{{n\left( {n + 1} \right)}} = \dfrac{1}{6}\\ \Leftrightarrow 6n - 6 = {n^2} + n\\ \Leftrightarrow {n^2} - 5n + 6 = 0 \Leftrightarrow \left[ \begin{array}{l}n = 3\,\,\left( {tm} \right)\\n = 2\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Nếu một đa giác đều có \(44\) đường chéo, thì số cạnh của đa giác là:
Số đoạn thẳng tạo bởi \(n\) đỉnh là \(C_n^2\), trong đó có \(n\) cạnh, suy ra số đường chéo là \(C_n^2 - n\).
Khi đó \(C_n^2 - n = 44 \Leftrightarrow \dfrac{{n!}}{{\left( {n - 2} \right)!.2!}} - n = 44\)
\( \Leftrightarrow n\left( {n - 1} \right) - 2n = 88 \Leftrightarrow \left[ \begin{array}{l}n = 11\\n = - 8\end{array} \right. \Leftrightarrow n = 11\) (vì \(n \in \mathbb{N}\)).
Tính \(B = \dfrac{1}{{A_2^2}} + \dfrac{1}{{A_3^2}} + ... + \dfrac{1}{{A_n^2}}\), biết \(C_n^1 + 2\dfrac{{C_n^2}}{{C_n^1}} + ... + n\dfrac{{C_n^n}}{{C_n^{n - 1}}} = 55\)
Ta có: \(C_n^1 = n\); \(2\dfrac{{C_n^2}}{{C_n^1}} = 2.\dfrac{{\dfrac{{n!}}{{2!.(n - 2)!}}}}{{\dfrac{{n!}}{{1!.(n - 1)!}}}} = n - 1\);...; \(n\dfrac{{C_n^n}}{{C_n^{n - 1}}} = n.\dfrac{1}{{\dfrac{{n!}}{{1!.(n - 1)!}}}} = 1\)
Nên \(C_n^1 + 2\dfrac{{C_n^2}}{{C_n^1}} + ... + n\dfrac{{C_n^n}}{{C_n^{n - 1}}} = 55\) \( \Leftrightarrow n + \left( {n - 1} \right) + \left( {n - 2} \right) + ... + 2 + 1 = 55\) \( \Leftrightarrow \dfrac{{n\left( {n + 1} \right)}}{2} = 55 \Leftrightarrow n = 10\)
Lại có: \(A_2^2 = 2! = 2.1\); \(A_3^2 = \dfrac{{3!}}{{\left( {3 - 2} \right)!}} = 3.2\); \(A_4^2 = \dfrac{{4!}}{{\left( {4 - 2} \right)!}} = 4.3\);…;\(A_{10}^2 = \dfrac{{10!}}{{\left( {10 - 2} \right)!}} = 10.9\)
\( \Rightarrow B = \dfrac{1}{{A_2^2}} + \dfrac{1}{{A_3^2}} + ... + \dfrac{1}{{A_{10}^2}}\) \(=\dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + ... + \dfrac{1}{{9.10}}\) \( = 1 - \dfrac{1}{2} + \dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + ... + \dfrac{1}{9} - \dfrac{1}{{10}} = 1 - \dfrac{1}{{10}} = \dfrac{9}{{10}}\)
Giá trị của $n$ thỏa mãn $3A_n^2 - A_{2n}^2 + 42 = 0$ là
* PP tự luận:
+ PT \( \Leftrightarrow 3.\dfrac{{n!}}{{\left( {n - 2} \right)!}} - \dfrac{{\left( {2n} \right)!}}{{\left( {2n - 2} \right)!}} + 42 = 0\,\,,\,\,\left( {n \in \mathbb{N},n \ge 2} \right)\)\( \Leftrightarrow 3n\left( {n - 1} \right) - 2n.\left( {2n - 1} \right) + 42 = 0\)\( \Leftrightarrow - {n^2} - n + 42 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}n = 6\,\left( {TM} \right)\\n = - 7\,\left( L \right)\end{array} \right.\)\( \Leftrightarrow n = 6\).
Tìm $x \in \mathbb{N}$, biết $C_x^0 + C_x^{x - 1} + C_x^{x - 2} = 79$
* PP tự luận:
PT \( \Leftrightarrow 1 + \dfrac{{x!}}{{\left( {x - 1} \right)!}} + \dfrac{{x!}}{{\left( {x - 2} \right)!2!}} = 79\,\left( {x \in \mathbb{N},\,x \ge 1} \right)\)\( \Leftrightarrow 1 + x + \dfrac{{\left( {x - 1} \right)x}}{2} = 79\)\( \Leftrightarrow {x^2} + x - 156 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = 12\left( {TM} \right)\\x = - 13\left( L \right)\end{array} \right. \Leftrightarrow x = 12\).
Tìm $n \in \mathbb{N}$, biết $C_{n + 4}^{n + 1} - C_{n + 3}^n = 7(n + 3)$.
* PP tự luận:
PT $ \Leftrightarrow \dfrac{{\left( {n + 4} \right)!}}{{3!\left( {n + 1} \right)!}} - \dfrac{{\left( {n + 3} \right)!}}{{3!n!}} = 7\left( {n + 3} \right)\,\,,\,\,n \in \mathbb{N}$\( \Leftrightarrow \dfrac{{\left( {n + 2} \right)\left( {n + 3} \right)\left( {n + 4} \right)}}{6} - \dfrac{{\left( {n + 1} \right)\left( {n + 2} \right)\left( {n + 3} \right)}}{6} = 7\left( {n + 3} \right)\)\( \Leftrightarrow \left( {n + 2} \right)\left( {n + 4} \right) - \left( {n + 1} \right)\left( {n + 2} \right) = 42\)\( \Leftrightarrow 3n + 6 = 42 \Leftrightarrow n = 12\).
Giá trị của $n \in \mathbb{N}$ bằng bao nhiêu, biết $\dfrac{5}{{C_5^n}} - \dfrac{2}{{C_6^n}} = \dfrac{{14}}{{C_7^n}}$.
* PP tự luận:
PT \( \Leftrightarrow \dfrac{5}{{\dfrac{{5!}}{{\left( {5 - n} \right)!n!}}}} - \dfrac{2}{{\dfrac{{6!}}{{\left( {6 - n} \right)!n!}}}} = \dfrac{{14}}{{\dfrac{{7!}}{{\left( {7 - n} \right)!n!}}}}\,\,,\,\,n \in \mathbb{N},0 \le n \le 5\)\( \Leftrightarrow \dfrac{{5.\left( {5 - n} \right)!n!}}{{5!}} - \dfrac{{2.\left( {6 - n} \right)!n!}}{{6!}} = \dfrac{{14.\left( {7 - n} \right)!n!}}{{7!}}\)\( \Leftrightarrow 5.6.7 - 2.7.\left( {6 - n} \right) = 14\left( {6 - n} \right)\left( {7 - n} \right)\)\( \Leftrightarrow 210 - 84 + 14n = 14{n^2} - 182n + 588\)\( \Leftrightarrow 14{n^2} - 196n + 462 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}n = 11\,\left( L \right)\\n = 3\,\left( {TM} \right)\end{array} \right. \Leftrightarrow n = 3\).
Biết $n$ là số nguyên dương thỏa mãn $3C_{n + 1}^3 - 3A_n^2 = 52(n - 1)$. Giá trị của $n$ bằng:
* PP tự luận:
PT \( \Leftrightarrow 3.\dfrac{{\left( {n + 1} \right)!}}{{\left( {n - 2} \right)!3!}} - 3.\dfrac{{n!}}{{\left( {n - 2} \right)!}} = 52\left( {n - 1} \right)\,\,,\,\,\left( {n \in \mathbb{N},n \ge 2} \right)\)$ \Leftrightarrow \dfrac{{\left( {n - 1} \right)n\left( {n + 1} \right)}}{2} - 3\left( {n - 1} \right)n = 52\left( {n - 1} \right)$$ \Leftrightarrow n\left( {n + 1} \right) - 6n = 104$$ \Leftrightarrow {n^2} - 5n - 104 = 0$\( \Leftrightarrow \left[ \begin{array}{l}n = 13\left( {TM} \right)\\n = - 8\left( L \right)\end{array} \right.\)\( \Leftrightarrow n = 13\).
Giải hệ phương trình sau:\(\left\{ \begin{array}{l}C_{x + 1}^{y + 1} = C_{x + 1}^y\\3C_{x + 1}^{y + 1} = 5C_{x + 1}^{y - 1}\end{array} \right.\)
Điều kiện \(x,y \in \mathbb{N};\,x \ge y\)
Ta có: \(\left\{ \begin{array}{l}C_{x + 1}^{y + 1} = C_{x + 1}^y\\3C_{x + 1}^{y + 1} = 5C_{x + 1}^{y - 1}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{(x + 1)!}}{{(y + 1)!(x - y)!}} = \dfrac{{(x + 1)!}}{{y!(x - y + 1)!}}\\3\dfrac{{(x + 1)!}}{{(y + 1)!(x - y)!}} = 5\dfrac{{(x + 1)!}}{{(y - 1)!(x - y + 2)!}}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}\dfrac{1}{{y + 1}} = \dfrac{1}{{x - y + 1}}\\\dfrac{3}{{y(y + 1)}} = \dfrac{5}{{(x - y + 1)(x - y + 2)}}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 2y\\3(y + 1)(y + 2) = 5y(y + 1)\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x = 2y\\3y + 6 = 5y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 6\\y = 3\end{array} \right.\) là nghiệm của hệ.
Giải bất phương trình sau:\(\dfrac{{{P_{x + 5}}}}{{(x - k)!}} \le 60A_{x + 3}^{k + 2}\)
Điều kiện: \(\left\{ \begin{array}{l}k,x \in \mathbb{N}\\k \le x\end{array} \right.\)
Bpt \( \Leftrightarrow (x + 4)(x + 5)(x + 1 - k) \le 60\)
\( \bullet \) \(x \ge 4 \Rightarrow \) bất phương trình vô nghiệm
\( \bullet \) \(0 \le x < 4\) ta có các cặp nghiệm: \((x;k) = (0;0),(1;0),(1;1),(2;2),(3;3)\).
Giải phương trình với ẩn số nguyên dương $n$ thỏa mãn $A_n^2 - 3C_n^2 = 15 - 5n$
* PP tự luận:
PT \( \Leftrightarrow \dfrac{{n!}}{{\left( {n - 2} \right)!}} - 3.\dfrac{{n!}}{{\left( {n - 2} \right)!2!}} = 15 - 5n\,\,,\,\,\left( {n \in \mathbb{N},n \ge 2} \right)\)\( \Leftrightarrow \left( {n - 1} \right)n - \dfrac{{3\left( {n - 1} \right)n}}{2} = 15 - 5n\)\( \Leftrightarrow - {n^2} + 11n - 30 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}n = 6\,\left( {TM} \right)\\n = 5\,\left( {TM} \right)\end{array} \right.\).
Tính \(M = \dfrac{{A_{n + 1}^4 + 3A_n^3}}{{\left( {n + 1} \right)!}}\), biết \(C_{n + 1}^2 + 2C_{n + 2}^2 + 2C_{n + 3}^2 + C_{n + 4}^2 = 149\).
Điều kiện: \(\left\{ \begin{array}{l}n \in \mathbb{N}\\n \ge 3\end{array} \right.\)
Ta có: \(C_{n + 1}^2 + 2C_{n + 2}^2 + 2C_{n + 3}^2 + C_{n + 4}^2 = 149\)
\( \Leftrightarrow \dfrac{{\left( {n + 1} \right)!}}{{2!\left( {n - 1} \right)!}} + 2\dfrac{{\left( {n + 2} \right)!}}{{2!n!}} + 2\dfrac{{\left( {n + 3} \right)!}}{{2!\left( {n + 1} \right)!}} + \dfrac{{\left( {n + 4} \right)!}}{{2!\left( {n + 2} \right)!}} = 149 \Leftrightarrow n = 5\)
Do đó: \(M = \dfrac{{A_6^4 + 3A_5^3}}{{6!}} = \dfrac{3}{4}\).
Giá trị của $n \in \mathbb{N}$ thỏa mãn đẳng thức $C_n^6 + 3C_n^7 + 3C_n^8 + C_n^9 = 2C_{n + 2}^8$ là
PP sử dụng máy tính để chọn đáp số đúng (PP trắc nghiệm):
+ Nhập PT vào máy tính: $C_n^6 + 3C_n^7 + 3C_n^8 + C_n^9 - 2C_{n + 2}^8 = 0$

+ Tính (CALC) lần lượt với \(X = 18\) (không thoả); với \(X = 16\) (không thoả); với \(X = 15\) (thoả), với \(X = 14\) (không thoả)

Tổng của ba số hạng liên tiếp lập thành cấp số cộng trong dãy số sau \(C_{23}^0;C_{23}^1; \ldots ;C_{23}^{13}\) có giá trị là
Giả sử 3 số \(C_{23}^n;C_{23}^{n + 1};C_{23}^{n + 2}\) theo thứ tự đó lập thành một cấp số cộng khi và chỉ khi \(2C_{23}^{n + 1} = C_{23}^n + C_{23}^{n + 2}\).
\(2C_{23}^{n + 1} + C_{23}^{n + 1} + C_{23}^{n + 1} = C_{23}^n + C_{23}^{n + 2} + C_{23}^{n + 1} + C_{23}^{n + 1}\)\( \Leftrightarrow 4C_{23}^{n + 1} = \left( {C_{23}^n + C_{23}^{n + 1}} \right) + \left( {C_{23}^{n + 1} + C_{23}^{n + 2}} \right)\)
\( \Leftrightarrow 4C_{23}^{n + 1} = C_{24}^{n + 1} + C_{24}^{n + 2}\)$ \Leftrightarrow 4C_{23}^{n + 1} = C_{25}^{n + 2}$
$ \Leftrightarrow \dfrac{{4.23!}}{{\left( {n + 1} \right)!\left( {22 - n} \right)!}} = \dfrac{{25!}}{{\left( {n + 2} \right)!\left( {23 - n} \right)!}}$.
$ \Rightarrow \left( {n + 2} \right)\left( {23 - n} \right) = 150 \Leftrightarrow \left[ \begin{array}{l}n = 8{\rm{ }}\left( {tm} \right)\\n = 13{\rm{ }}\left( l \right)\end{array} \right.$.
Vậy \(C_{23}^8 + C_{23}^9 + C_{23}^{10} = 2451570\).
Nếu \(2A_n^4 = 3A_{n - 1}^4\) thì \(n\) bằng
Cách 1:
Bước 1:
Vì nên \(n - 1 \ge 4 \Leftrightarrow n \ge 5\).
Bước 2:
Ta có: \(2A_n^4 = 3A_{n - 1}^4 \Leftrightarrow 2.\dfrac{{n!}}{{\left( {n - 4} \right)!}} = 3.\dfrac{{\left( {n - 1} \right)!}}{{\left( {n - 5} \right)!}}\)
Bước 3:
\( \Leftrightarrow 2n\left( {n - 1} \right)\left( {n - 2} \right)\left( {n - 3} \right) = 3.\left( {n - 1} \right)\left( {n - 2} \right)\left( {n - 3} \right)\left( {n - 4} \right)\)
\( \Leftrightarrow 2n = 3\left( {n - 4} \right) \Leftrightarrow 2n = 3n - 12 \Leftrightarrow n = 12\).
Cách 2:
Có thể sử dụng cách thử đáp án bằng MTCT, chức năng CALC.
Bước 1: Nhập vào màn hình \(2\left( {XP4} \right) - 3\left( {\left( {X - 1} \right)P4} \right)\)
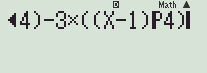
Bước 2: Bấm CALC

Bước 3: Nhập các giá trị ở mỗi đáp án rồi ấn “=”, nếu được kết quả bằng \(0\) thì chọn.
Đáp án A:

Kết quả:
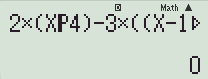
Cho \(n\) là số nguyên dương và \(C_n^5 = 792.\) Tính \(A_n^5.\)
Ta có \(A_n^5 = 5!.C_n^5 = 5!.792 = 95040\).
Nếu \(A_x^2 = 110\)thì:
\(A_x^2 = 110\)\((x \ge 2)\)
\( \Leftrightarrow \dfrac{{x!}}{{\left( {x - 2} \right)!}} = 110\)
\( \Leftrightarrow x(x - 1) = 110\)
\( \Leftrightarrow {x^2} - x - 110 = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}x = 11\,\,\,\,\,\,\left( {tm} \right)\\x = - 10\,\,\left( {ktm} \right)\end{array} \right.\)
Vậy \(x = 11\).
Nếu \(2A_n^4 = 3A_{n - 1}^4\) thì \(n\) bằng:
\(2A_n^4 = 3A_{n - 1}^4\) \(\left( {n \ge 5;\,\,n \in N} \right)\)
\( \Leftrightarrow 2\dfrac{{n!}}{{\left( {n - 4} \right)!}} = 3\dfrac{{\left( {n - 1} \right)!}}{{\left( {n - 5} \right)!}}\)
\( \Leftrightarrow 2n\left( {n - 1} \right)\left( {n - 2} \right)\left( {n - 3} \right) - 3\left( {n - 1} \right)\left( {n - 2} \right)\left( {n - 3} \right)\left( {n - 4} \right) = 0\)
\( \Leftrightarrow \left( {n - 1} \right)\left( {n - 2} \right)\left( {n - 3} \right)\left[ {2n - 3\left( {n - 4} \right)} \right] = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}n = 1\,\,\,\,\left( {ktm} \right)\\n = 2\,\,\,\left( {ktm} \right)\\n = 3\,\,\,\,\left( {ktm} \right)\\2n - 3n + 12 = 0\end{array} \right. \Leftrightarrow n = 12\,\,\left( {tm} \right)\)
Nghiệm của phương trình \(A_x^{10} + A_x^9 = 9A_x^8\) là:
\(A_x^{10} + A_x^9 = 9A_x^8\) \(\left( {x \ge 10;\,\,x \in {N^*}} \right)\)
\( \Leftrightarrow \dfrac{{x!}}{{\left( {x - 10} \right)!}} + \dfrac{{x!}}{{\left( {x - 9} \right)!}} = 9\dfrac{{x!}}{{\left( {x - 8} \right)!}}\)
\( \Leftrightarrow x\left( {x - 1} \right)\left( {x - 2} \right)...\left( {x - 9} \right) + x\left( {x - 1} \right)\left( {x - 2} \right)...\left( {x - 8} \right) = 9x\left( {x - 1} \right)\left( {x - 2} \right)...\left( {x - 7} \right)\)
\( \Leftrightarrow \left( {x - 8} \right)\left( {x - 9} \right) + \left( {x - 8} \right) = 9\)
\( \Leftrightarrow {x^2} - 9x - 8x + 72 + x - 8 - 9 = 0\)
\( \Leftrightarrow {x^2} - 16x + 55 = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}x = 11\,\,\,\,\left( {tm} \right)\\x = 5\,\,\,\,\,\left( {ktm} \right)\end{array} \right.\) .
Với \(\dfrac{{\left( {n + 1} \right)!}}{{\left( {n - 1} \right)!}} = 72\) thì giá trị của $n$ là:
ĐK: \(n \in N,n > 1\)
\(\dfrac{{\left( {n + 1} \right)!}}{{\left( {n - 1} \right)!}} = 72 \Leftrightarrow n\left( {n + 1} \right) = 72 \Leftrightarrow {n^2} + n - 72 = 0 \Leftrightarrow \left[ \begin{array}{l}n = 8\,\,\,\,\,\,\left( {tm} \right)\\n = - 9\,\,\left( {ktm} \right)\end{array} \right.\)

