Trả lời bởi giáo viên
Đáp án đúng: a
Cách 1:
Bước 1:
Vì nên n−1≥4⇔n≥5.
Bước 2:
Ta có: 2A4n=3A4n−1⇔2.n!(n−4)!=3.(n−1)!(n−5)!
Bước 3:
⇔2n(n−1)(n−2)(n−3)=3.(n−1)(n−2)(n−3)(n−4)
⇔2n=3(n−4)⇔2n=3n−12⇔n=12.
Cách 2:
Có thể sử dụng cách thử đáp án bằng MTCT, chức năng CALC.
Bước 1: Nhập vào màn hình 2(XP4)−3((X−1)P4)
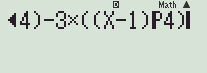
Bước 2: Bấm CALC

Bước 3: Nhập các giá trị ở mỗi đáp án rồi ấn “=”, nếu được kết quả bằng 0 thì chọn.
Đáp án A:

Kết quả:
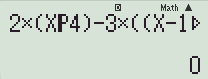
Hướng dẫn giải:
Bước 1: Tìm điều kiện của n bằng cách sử dụng điều kiện nếu có Akn thì n≥k
Bước 2: Sử dụng công thức Akn=n!(n−k)! đưa về phương trình ẩn n.
Bước 3: Giải phương trình, loại các trường hợp n<5.

