Đặt điện áp xoay chiều có giá trị cực đại là \(220\sqrt 2 V\) vào hai đầu một tụ điện thì cường độ dòng điện trong cuộn cảm có biểu thức \(i = 5.\cos 100\pi t\,\,\left( A \right)\). Tại thời điểm điện áp có 220V và đang tăng thì cường độ dòng điện là:
Đối với đoạn mạch chỉ chứa tụ điện thì điện áp hai đầu mạch luôn trễ pha hơn so với dòng điện một góc \(\dfrac{\pi }{2}\)
Biểu diễn trên VTLG ta có:
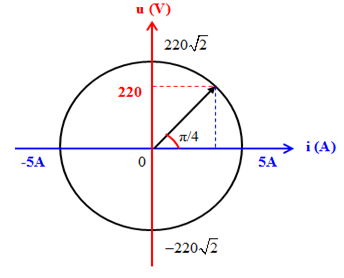
Từ VTLG ta thấy tại thời điểm u = 220V và đang tăng thì cường độ dòng điện:
\(i = {I_0}.\cos \dfrac{\pi }{4} = 5.\dfrac{{\sqrt 2 }}{2} = 2,5\sqrt 2 A\)
Cho cường độ dòng điện tức thời của đoạn mạch xoay chiều là \(i = 5\cos \left( {120\pi t - \dfrac{\pi }{3}} \right)A\). Khi đó
- Tần số của dòng điện là:
\(f = \frac{\omega }{{2\pi }} = \dfrac{{120\pi }}{{2\pi }} = 60Hz\) => A sai
- Cường độ dòng điện cực đại là:
\({I_0} = 5{\rm{A}}\) => B sai
- Pha dao động của dòng điện là \(\left( {120\pi t - \dfrac{\pi }{3}} \right)\) => C sai
- Cường độ dòng điện hiệu dụng: \(I = \dfrac{{{I_0}}}{{\sqrt 2 }} = \dfrac{5}{{\sqrt 2 }}A\) => D đúng
Đặt điện áp \(u = {U_0}\cos \left( {\omega t + \dfrac{\pi }{3}} \right)\) vào hai đầu cuộn cảm thuần có độ tự cảm \(L\) thì cường độ dòng điện qua cuộn cảm là
Biểu thức của điện áp: \(u = {U_0}\cos \left( {\omega t + \dfrac{\pi }{3}} \right)\)
Biểu thức của cường độ dòng điện qua cuộn cảm thuần:
\(i = \dfrac{{{U_0}}}{{{Z_L}}}\cos \left( {\omega t + \dfrac{\pi }{3} - \dfrac{\pi }{2}} \right) = \dfrac{{{U_0}}}{{\omega L}}\cos \left( {\omega t - \dfrac{\pi }{6}} \right)\)
Điện áp \(u = 200co{\rm{s}}\left( {100\pi t + \frac{\pi }{2}} \right)\left( V \right)\) có giá trị hiệu dụng bằng
Điện áp hiệu dụng: \(U = \dfrac{{{U_0}}}{{\sqrt 2 }} = \dfrac{{200}}{{\sqrt 2 }} = 100\sqrt 2 V\)
Một học sinh xác định điện dung của tụ điện bằng cách đặt điện áp \(u = {U_0}.cos\omega t\) (U0 không đổi, \(\omega = 314rad/s\)) vào hai đầu một đoạn mạch gồm tụ điện có điện dung C mắc nối tiếp với biến trở R. Biết \(\dfrac{1}{{{U^2}}} = \dfrac{2}{{U_0^2}} + \dfrac{2}{{U_0^2{\omega ^2}{C^2}}}.\dfrac{1}{{{R^2}}}\); trong đó điện áp U giữa hai đầu R được đo bằng đồng hồ đo điện đa năng hiện số. Dựa vào kết quả thực nghiệm đo được trên hình vẽ, học sinh này tính được giá trị của C là:
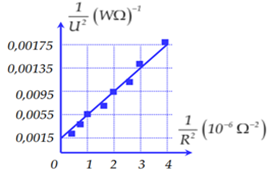
+ Tại: \(\dfrac{1}{{{R^2}}} = {10^{ - 6}}\) thì \(\dfrac{1}{{{U^2}}} = 0,0055\) ta có:
\(\dfrac{1}{{{U^2}}} = \dfrac{2}{{U_0^2}} + \dfrac{2}{{U_0^2.{\omega ^2}.{C^2}}}.\dfrac{1}{{{R^2}}} \Leftrightarrow 0,0055 = \dfrac{2}{{U_0^2}} + \dfrac{{{{2.10}^{ - 6}}}}{{U_0^2.{\omega ^2}.{C^2}}}\)
+ Tại: \(\dfrac{1}{{{R^2}}} = {2.10^{ - 6}}\) thì \(\dfrac{1}{{{U^2}}} = 0,0095\)ta có:
\(\dfrac{1}{{{U^2}}} = \dfrac{2}{{U_0^2}} + \dfrac{2}{{U_0^2.{\omega ^2}.{C^2}}}.\dfrac{1}{{{R^2}}} \Leftrightarrow 0,0095 = \dfrac{2}{{U_0^2}} + \dfrac{{{{4.10}^{ - 6}}}}{{U_0^2.{\omega ^2}.{C^2}}}\)
Ta được hệ phương trình:
\(\left\{ {\begin{array}{*{20}{l}}{0,0055 = \dfrac{2}{{U_0^2}} + \dfrac{2}{{U_0^2.{\omega ^2}.{C^2}}}{{.10}^{ - 6}}}\\{0,0095 = \dfrac{2}{{U_0^2}} + \dfrac{2}{{U_0^2.{\omega ^2}.{C^2}}}{{.2.10}^{ - 6}}}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{0,0055 = \dfrac{2}{{U_0^2}}.\left( {1 + \dfrac{1}{{3,{{14}^2}.{C^2}}}{{.10}^{ - 6}}} \right){\mkern 1mu} \,\,\,{\mkern 1mu} \left( 1 \right)}\\{0,0095 = \dfrac{2}{{U_0^2}}\left( {1 + \dfrac{1}{{3,{{14}^2}.{C^2}}}{{.2.10}^{ - 6}}} \right){\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 2 \right)}\end{array}} \right.\)
Lấy (2) chia (1) ta được: \(C = 1,{95.10^{ - 4}}F\)

