Một học sinh xác định điện dung của tụ điện bằng cách đặt điện áp \(u = {U_0}.cos\omega t\) (U₀ không đổi, \(\omega  = 314rad/s\)) vào hai đầu một đoạn mạch gồm tụ điện có điện dung C mắc nối tiếp với biến trở R. Biết \(\dfrac{1}{{{U^2}}} = \dfrac{2}{{U_0^2}} + \dfrac{2}{{U_0^2{\omega ^2}{C^2}}}.\dfrac{1}{{{R^2}}}\); trong đó điện áp U giữa hai đầu R được đo bằng đồng hồ đo điện đa năng hiện số. Dựa vào kết quả thực nghiệm đo được trên hình vẽ, học sinh này tính được giá trị của C là:

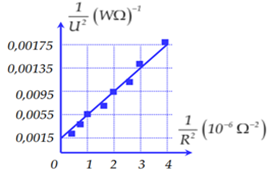
+ Tại: \(\dfrac{1}{{{R^2}}} = {10^{ - 6}}\) thì \(\dfrac{1}{{{U^2}}} = 0,0055\) ta có:

\(\dfrac{1}{{{U^2}}} = \dfrac{2}{{U_0^2}} + \dfrac{2}{{U_0^2.{\omega ^2}.{C^2}}}.\dfrac{1}{{{R^2}}} \Leftrightarrow 0,0055 = \dfrac{2}{{U_0^2}} + \dfrac{{{{2.10}^{ - 6}}}}{{U_0^2.{\omega ^2}.{C^2}}}\)

+ Tại: \(\dfrac{1}{{{R^2}}} = {2.10^{ - 6}}\) thì  \(\dfrac{1}{{{U^2}}} = 0,0095\)ta có:

\(\dfrac{1}{{{U^2}}} = \dfrac{2}{{U_0^2}} + \dfrac{2}{{U_0^2.{\omega ^2}.{C^2}}}.\dfrac{1}{{{R^2}}} \Leftrightarrow 0,0095 = \dfrac{2}{{U_0^2}} + \dfrac{{{{4.10}^{ - 6}}}}{{U_0^2.{\omega ^2}.{C^2}}}\)

Ta được hệ phương trình:

\(\left\{ {\begin{array}{*{20}{l}}{0,0055 = \dfrac{2}{{U_0^2}} + \dfrac{2}{{U_0^2.{\omega ^2}.{C^2}}}{{.10}^{ - 6}}}\\{0,0095 = \dfrac{2}{{U_0^2}} + \dfrac{2}{{U_0^2.{\omega ^2}.{C^2}}}{{.2.10}^{ - 6}}}\end{array}} \right.\)

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{0,0055 = \dfrac{2}{{U_0^2}}.\left( {1 + \dfrac{1}{{3,{{14}^2}.{C^2}}}{{.10}^{ - 6}}} \right){\mkern 1mu} \,\,\,{\mkern 1mu} \left( 1 \right)}\\{0,0095 = \dfrac{2}{{U_0^2}}\left( {1 + \dfrac{1}{{3,{{14}^2}.{C^2}}}{{.2.10}^{ - 6}}} \right){\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 2 \right)}\end{array}} \right.\)

Lấy (2) chia (1) ta được: \(C = 1,{95.10^{ - 4}}F\)