Bài tập phương trình dao động mạch LC (q - u - i)

Ta có khoảng thời gian để cường độ dòng điện trong mạch giảm từ I₀ đến I₀/2 là: \(\tau  = \frac{T}{6} = \frac{8}{3}\mu s \to T = 16\mu s\) 

Tần số góc: \(\omega  = \frac{{2\pi }}{T} = \frac{{2\pi }}{{{{16.10}^{ - 6}}}} = 12,5\pi {.10^4}(ra{\rm{d}}/s)\) 

- Khi i = 0 thì q = q₀ : do cường độ dòng điện và điện tích lệch pha nhau một góc π/2

Ta có, \({q_0} = \frac{{{I_0}}}{\omega } = \frac{{2,22}}{{12,5\pi {{.10}^4}}} = 5,{65.10^{ - 6}}C\)

Chu kỳ mạch dao động LC là: \(T = 2\pi \sqrt {LC}  = 2\pi \sqrt {{{8.10}^{ - 3}}{{.2.10}^{ - 9}}}  = 8\pi {.10^{ - 6}}(s) \Rightarrow \omega  = 2,{5.10^5}rad/s\)

Ta có: \(CU_0^2 = LI_0^2 \Rightarrow {U_0} = \sqrt {\dfrac{{LI_0^2}}{C}}  = 2000{I_0}\)

Z_L = 2000Ω; Z_C = 2000Ω nên u và i cùng pha nhau

Ở thời điểm t₁ có i₁ = ωq₀cos(ωt₁) = ωCU₀cos(ωt₁) = 5mA

Ở thời điểm t₂ có u₂ = \({U_0}{\rm{cos}}\left[ {\omega ({t_1} + \dfrac{T}{4}) - \dfrac{\pi }{2}} \right] = {U_0}{\rm{cos}}\omega {{\rm{t}}_1} = \dfrac{{{i_1}}}{{\omega C}} = \dfrac{{{{5.10}^{ - 3}}}}{{2,{{5.10}^5}{{.2.10}^{ - 9}}}} = 10V\)

Ta có, tại thời điểm t cường độ dòng điện \(i = 0A\)  (có thể ở vị trí 1 hoặc 2 như hình vẽ)

Ở thời điểm \(t + \dfrac{{\pi \sqrt {LC} }}{2} = t + \dfrac{T}{4}\)

+ Ứng với vị trí 1 => tại thời điểm \(t + \dfrac{T}{4}\) cường độ dòng điện \(i = {I_0}\)

+ Ứng với vị trí 2 => tại thời điểm \(t + \dfrac{T}{4}\) cường độ dòng điện \(i =  - {I_0}\)

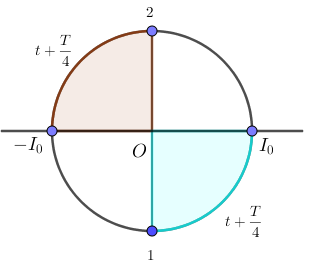
\(\Rightarrow \left| i \right| = {I_0}\) và \(u = 0,q = 0\)

\( \Rightarrow \) Năng lượng điện trường: \({{\rm{W}}_d} = \dfrac{{{q^2}}}{{2C}} = 0\)

Biểu thức điện tích: \(q = {q_0}co{\rm{s}}\left( {\omega t + \frac{\pi }{2}} \right)\left( C \right)\)

Tại \(t = 0\) có \(q = 0\)

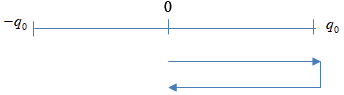
Thời gian ngắn nhất kể từ \(t = 0\) đến khi điện tích trên tụ bằng 0 là:

\(\Delta t = \frac{T}{2} = {10^{ - 6}}s \Rightarrow T = {2.10^{ - 6}}s\)

Tần số: \(f = \frac{1}{T} = 500000H{\rm{z}} = 500kH{\rm{z}}\)

Ta có:

\(\omega  = \frac{1}{{\sqrt {LC} }} \Leftrightarrow 100\pi  = \frac{1}{{\sqrt {{{2.10}^{ - 3}}.C} }}\)

\( \Rightarrow C = {5.10^{ - 3}}F\)

Lại có:

\(\frac{{LI_0^2}}{2} = \frac{{Q_0^2}}{{2C}} \Leftrightarrow Q_0^2 = LI_0^2C\)

\({Q_0} = {I_0}\sqrt {LC}  = 0,05.\frac{1}{{100\pi }} = \frac{{{{5.10}^{ - 4}}}}{\pi }\left( C \right)\)

Mặt khác, q trễ pha hơn i góc \(\frac{\pi }{2}\) suy ra \({\varphi _q} = 0 - \frac{\pi }{2} =  - \frac{\pi }{2}\)

Vậy \(q = \frac{{{{5.10}^{ - 4}}}}{\pi }\cos \left( {100\pi t - \frac{\pi }{2}} \right)\left( C \right)\)

Năng lượng trên tụ điện dao động với tần số góc \(\omega  = \dfrac{2}{{\sqrt {LC} }}\)

\( \Rightarrow \) Tần số góc \(\omega  = \dfrac{1}{{\sqrt {LC} }}\) không phải là tần số của năng lượng tụ điện.

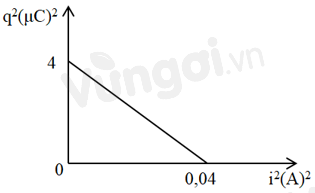
Từ đồ thị ta thấy:

+ Tại \(\left\{ \begin{array}{l}{i^2} = 0\\{q^2} = 4{\left( {\mu C} \right)^2}\end{array} \right. \Rightarrow Q_0^2 = 4{\left( {\mu C} \right)^2} \Rightarrow {Q_0} = 2\mu C\)

+ Tại: \(\left\{ {\begin{array}{*{20}{l}}{{q^2} = 0}\\{{i^2} = 0,04{\mkern 1mu} {\mkern 1mu} {{\left( A \right)}^2}}\end{array}} \right. \Rightarrow I_0^2 = 0,04{\mkern 1mu} {\mkern 1mu} {\left( A \right)^2} \Rightarrow {I_0} = 0,2{\mkern 1mu} {\mkern 1mu} \left( A \right)\)

\( \Rightarrow \omega {\rm{}} = \dfrac{{{I_0}}}{{{Q_0}}} = \dfrac{{0,2}}{{{{2.10}^{ - 6}}}} = {1.10^5}{\mkern 1mu} {\mkern 1mu} \left( {rad/s} \right)\)

Bước sóng mà mạch thu được trong không khí là:

\(\lambda  = \dfrac{{2\pi c}}{\omega } = \dfrac{{2\pi {{.3.10}^8}}}{{{{1.10}^5}}} = 6\pi {.10^3}\,\,\left( m \right)\)

Thời điểm ban đầu, tụ được nạp đầy điện và bắt đầu phóng điện, điện tích trên tụ giảm dần.

Ta có biểu thức: \(q = {Q_0}.\cos \left( {\omega t} \right)\)

Chu kì dao động của mạch:

\(T = 2\pi \sqrt {LC}  = 2\pi \sqrt {0,{{202.10}^{ - 6}}.0,5}  = {2.10^{ - 3}}s\)

Biểu diễn trên VTLG:

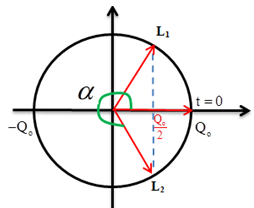
Góc quét tương ứng: \(\alpha  = 2\pi  - \dfrac{\pi }{3} = \dfrac{{5\pi }}{3}\)

\( \Rightarrow \) Lần thứ hai điện tích trên tụ bằng một nửa điện tích lúc đầu là:

\(t = \dfrac{\alpha }{\omega } = \alpha .\dfrac{T}{{2\pi }} = \dfrac{{5\pi }}{3}.\dfrac{{{{2.10}^{ - 3}}}}{{2\pi }} = \dfrac{1}{{600}}s\)