Câu hỏi:
2 năm trước
Một mạch dao động LC lí tưởng với \(q\) là điện tích trên tụ, \(i\) là dòng điện tức thời trong mạch. Đồ thị thể hiện sự phụ thuộc của \({q^2}\) vào \({i^2}\) như hình vẽ. Bước sóng mà mạch thu được trong không khí là
Trả lời bởi giáo viên
Đáp án đúng: d
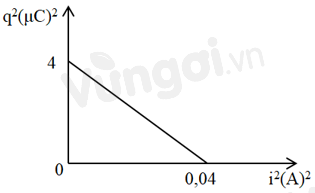
Từ đồ thị ta thấy:
+ Tại \(\left\{ \begin{array}{l}{i^2} = 0\\{q^2} = 4{\left( {\mu C} \right)^2}\end{array} \right. \Rightarrow Q_0^2 = 4{\left( {\mu C} \right)^2} \Rightarrow {Q_0} = 2\mu C\)
+ Tại: \(\left\{ {\begin{array}{*{20}{l}}{{q^2} = 0}\\{{i^2} = 0,04{\mkern 1mu} {\mkern 1mu} {{\left( A \right)}^2}}\end{array}} \right. \Rightarrow I_0^2 = 0,04{\mkern 1mu} {\mkern 1mu} {\left( A \right)^2} \Rightarrow {I_0} = 0,2{\mkern 1mu} {\mkern 1mu} \left( A \right)\)
\( \Rightarrow \omega {\rm{}} = \dfrac{{{I_0}}}{{{Q_0}}} = \dfrac{{0,2}}{{{{2.10}^{ - 6}}}} = {1.10^5}{\mkern 1mu} {\mkern 1mu} \left( {rad/s} \right)\)
Bước sóng mà mạch thu được trong không khí là:
\(\lambda = \dfrac{{2\pi c}}{\omega } = \dfrac{{2\pi {{.3.10}^8}}}{{{{1.10}^5}}} = 6\pi {.10^3}\,\,\left( m \right)\)
Hướng dẫn giải:
+ Biểu điện điện tích và cường độ dòng điện: \(\left\{ \begin{array}{l}q = {Q_0}.cos\left( {\omega t + \varphi } \right)\\i = {I_0}.cos\left( {\omega t + \varphi + \frac{\pi }{2}} \right)\end{array} \right.\)
+ Biểu thức vuông pha của q và i: \({\left( {\dfrac{q}{{{Q_0}}}} \right)^2} + {\left( {\dfrac{i}{{{I_0}}}} \right)^2} = 1\)
+ Mối liên hệ giữa điện tích cực đại và cường độ dòng điện cực đại: \({I_0} = \omega {Q_0}\)
+ Bước sóng: \(\lambda = \dfrac{{2\pi c}}{\omega }\)
Câu hỏi khác
- Bài tập mạch dao động LC các đại lượng đặc trưng có lời giải MÔN LÝ lớp 12
- Bài tập năng lượng của mạch dao động LC có lời giải MÔN LÝ lớp 12
- Bài tập phương trình dao động mạch LC q,u,i có lời giải MÔN LÝ lớp 12
- Bài tập điện từ trường - sóng điện từ lý 12 có lời giải
- Bài tập các loại dao động lý 12 có lời giải
