Hạt nhân Đơteri có khối lượng \({m_D} = {\rm{ }}2,0136u\), khối lượng của các nuclôn lần lượt là \({m_n} = {\rm{ }}1,0087u\), \({m_p} = {\rm{ }}1,0073u\). Biết \(u{c^2} = 931,5MeV\). Năng lượng liên kết riêng của hạt nhân Đơteri là:
+ Hạt nhân đơteri có kí hiệu: \({}_1^2D\)
=> hạt nhân đơteri có 1 hạt proton, 1 hạt notron.
+ Năng lượng liên kết của hạt nhân đơteri là:
\(\begin{array}{l}{{\rm{W}}_{lk}} = \Delta m{c^2} = \left( {Z{m_p} + \left( {A - Z} \right){m_n} - {m_D}} \right){c^2}\\ = \left( {1,0073u + 1,0087u - 2,0136u} \right){c^2}\\ = 2,{4.10^{ - 3}}u{c^2} = 2,2356MeV\end{array}\)
=> Năng lượng liên kết riêng của đơteri là: \(\varepsilon = \dfrac{{{{\rm{W}}_{lk}}}}{A} = \dfrac{{2,2356}}{2} = 1,1178MeV/nuclon\)
Cho biết \({m_\alpha } = 4,0015u\); \({m_C} = 12,000u\) \({m_O} = {\rm{ }}15,999u\), \({m_p} = {\rm{ }}1,007276u\), \({m_n} = {\rm{ }}1,008667u\) . Cho \(1u{\rm{ }} = {\rm{ }}931MeV/{c^2}\). Hãy sắp xếp các hạt nhân \({}_2^4He,{}_6^{12}C,{}_8^{16}O\) theo thứ tự tăng dần độ bền vững. Đáp án đúng là:
Năng lượng liên kết riêng của :
\({\varepsilon _{He}} = \dfrac{{\left[ {2.\left( {1,007276 + 1,008667} \right) - 4,0015} \right].931}}{4} = 7,07\,MeV\)
\({\varepsilon _O} = \dfrac{{\left[ {8.\left( {1,007276 + 1,008667} \right) - 15,999} \right].931}}{{16}} = 7,48\,MeV\)
\({\varepsilon _C} = \dfrac{{\left[ {6.\left( {1,007276 + 1,008667} \right) - 12} \right].931}}{{12}} = 7,42\,MeV\)
\( \Rightarrow {\varepsilon _{He}} < {\varepsilon _C} < {\varepsilon _O}\)
=> Theo thứ tự tăng dần độ bền vững: \(He, C, O\)
Hạt nhân \({}_2^4He\) có năng lượng liên kết là \(28,4MeV\); hạt nhân \({}_3^7Li\) có năng lượng liên kết là \(39,2MeV\); hạt nhân \({}_1^2D\) có năng lượng liên kết là \(2,24MeV\). Hãy sắp theo thứ tự tăng dần về tính bền vững của chúng:
Năng lượng liên kết riêng của:
\({\varepsilon _{He}} = \dfrac{{28,4}}{4} = 7,1{\rm{ }}MeV\); \({\varepsilon _{Li}} = \dfrac{{39,2}}{7} = {\rm{ }}5,6{\rm{ }}MeV\); \({\varepsilon _D} = \dfrac{{2,24}}{2} = 1,12{\rm{ }}MeV\)
\( \Rightarrow {\varepsilon _D} < {\varepsilon _{Li}} < {\varepsilon _{He}}\)
=> Theo thứ tự tăng dần về tính bền vững: \(D, Li, He\)
Hạt nhân nào sau đây bền vững nhất?
Các hạt nhân bền vững có \(\dfrac{{{{\rm{W}}_{lk}}}}{A}\) lớn nhất vào cỡ 8,8 MeV/nuclon; đó là những hạt nhân nằm khoảng giữa của bảng tuần hoàn ứng với 50 < A < 95
Hạt nhân \({}_{26}^{56}Fe\) có số khối A = 56
=> Hạt nhân bền vững nhất trong các hạt nhân trên là \({\rm{ }}_{26}^{56}F{\rm{e}}\)
Trên hình là đồ thị biểu diễn sự biến thiên của năng lượng liên kết riêng (trục tung, theo đơn vị MeV/nuclôn) theo số khối (trục hoành) của các hạt nhân nguyên tử. Phát biểu nào sau đây đúng?
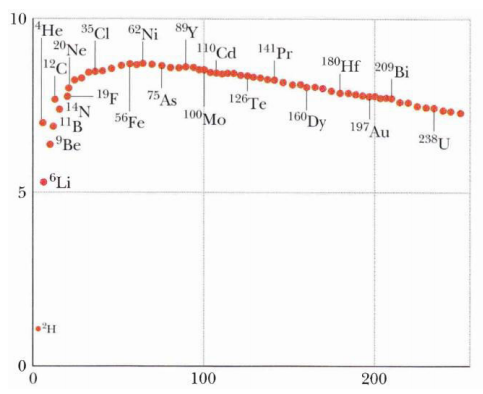
Hạt nhân 62Ni có năng lượng liên kết riêng lớn nhất: bền vững nhất.
Cho các khối lượng: hạt nhân \({}_{17}^{37}Cl\) ; nơtrôn; prôtôn lần lượt là 36,9566u; 1,0087u; 1,0073u. Độ hụt khối của hạt nhân \({}_{17}^{37}Cl\) bằng
Độ hụt khối của hạt nhân \({}_{17}^{37}Cl\) bằng:
\(\begin{array}{l}\Delta {m_X} = Z.{m_p} + \left( {A - Z} \right){m_n} - {m_X}\\\,\,\,\,\,\,\,\,\,\,\, = 17.1,0073 + \left( {37 - 17} \right).1,0087 - 36,9566 = 0,3415u\end{array}\)
Hạt nhân \({}_3^7{\rm{Li}}\) có khối lượng \(7,0144 u\). Cho khối lượng của prôtôn và nơtron lần lượt là \(1,0073 u\) và \(1,0087 u\). Độ hụt khối của hạt nhân \({}_3^7{\rm{Li}}\) là:
Độ hụt khối của hạt nhân Liti được xác định bởi biểu thức
\(\Delta m = Z{m_p} + N{m_n} - {m_{Li}} = 3.1,0073 + 4.1,0087 - 7,0144 = 0,0423u\)
Đại lượng đặc trưng cho mức độ bền vững của hạt nhân là
Năng lượng liên kết riêng đặc trưng cho mức độ bền vững của hạt nhân
Hạt nhân \(_8^{17}O\) có khối lượng 16,9947u. Biết khối lượng của prôtôn và notron lần lượt là 1,0073 u và 1,0087 u. Độ hụt khối của \(_8^{17}O\) là
Độ hụt khối:
\(\Delta m= Zm_p+(A-Z)m_n-m_{hn}\\=8m_p+9m_n-m_O\\=8.1,0073u+9.1,0087u-16,9947u=0,142u\)
Cho khối lượng của hạt nhân \({}_{47}^{107}Ag\) là \(106,8783u\); của notron là \(1,0087u\); của proton là \(1,0073u\). Độ hụt khối của hạt nhân \({}_{47}^{107}Ag\) là
Độ hụt khối của hạt nhân \({}_{47}^{107}Ag\) là:
\(\begin{array}{l}\Delta m = Z.{m_p} + \left( {A - Z} \right).{m_n} - m\\ \Rightarrow \Delta m = 47.1,0073u + \left( {107 - 47} \right).1,0087u - 106,8783u = 0,9868u\end{array}\)
Cho biết khối lượng hạt nhân \({}_{92}^{234}U\) là 233,9904 u. Biết khối lượng của hạt prôtôn và nơtrôn lần lượt là mp= 1,007276 u và mn = 1,008665 u. Độ hụt khối của hạt nhân \({}_{92}^{234}U\) bằng
Độ hụt khối của hạt nhân \({}_{92}^{234}U\) bằng:
\(\Delta m = 92.1,007276 + \left( {234 - 92} \right).1,008665 - 233,9904 = 1,909422u\)
Cho hạt \(\alpha \,\,\left( {{}_2^4He} \right)\) có khối lượng 4,0015u. Biết \({m_p} = 1,0072u;{m_n} = 1,0086u;1u = 931,5{\rm{ }}MeV/c\). Năng lượng liên kết riêng của hạt α là
Năng lượng liên kết của hạt α:
\(\begin{array}{l}
{{\rm{W}}_{lk}} = \left[ {Z.{m_p} + \left( {A - Z} \right).{m_n} - {m_X}} \right].{c^2}\\
\,\,\,\,\,\,\,\,\, = \left[ {2.1,0072 + 2.1,0086 - 4,0015} \right].931,5 = 28,04MeV
\end{array}\)
Năng lượng liên kết riêng của hạt α là :
\({{\rm{w}}_{lkr}} = \frac{{{{\rm{W}}_{lk}}}}{A} = \frac{{28,04}}{4} = 7,{01_{}}(Mev/nuclon)\)
Khối lượng của hạt nhân \({}_5^{10}B\) là 10,0102 u. Năng lượng liên kết của hạt nhân này bằng
Năng lượng liên kết của hạt nhân này bằng:
\(\begin{array}{l}
{{\rm{W}}_{lk}} = \left[ {Z.{m_p} + (A - Z).{m_n} - {m_X}} \right].{c^2}\\
\,\,\,\,\,\, = \left[ {Z.{m_p} + (A - Z).{m_n} - {m_X}} \right].{c^2}.931\left( {MeV} \right)\\
\,\,\,\,\,\, = \left[ {5.1,0072 + (10 - 5).1,0086 - 10,0102} \right].931,5 = 64,74meV
\end{array}\)
Khối lượng của hạt nhân \(_4^{10}Be\) là \(10,0113u\); khối lượng của proton là \(1,0072u\) và của notron là \(1,0086u\); \(1u = 931 MeV/c^2\). Năng lượng liên kết của\(_4^{10}Be\) là
Năng lượng liên kết của hạt nhân \(_4^{10}Be\) là:
\(W_{lk} = (4.1,0072 + 6.1,0086 – 10,0113).931 = 64,3 MeV\)
Trong các hạt nhân nguyên tử: \(_{\rm{2}}^{\rm{4}}{\rm{He; }}_{{\rm{26}}}^{{\rm{56}}}{\rm{Fe; }}_{{\rm{92}}}^{{\rm{238}}}{\rm{U}}\) và \(_{{\rm{90}}}^{{\rm{230}}}{\rm{Th,}}\) hạt nhân bền vững nhất là
Hạt nhân bền vững nhất có số khối nằm trong khoảng từ \(50\) đến \(80\).
Nên hạt nhân \(_{26}^{56}Fe\) bền vững nhất trong các hạt nhân ở trên
Đề thi THPT QG - 2020
Hạt nhân \(_5^{11}B\) có khối lượng 11,0066u. Cho khối lượng của proton và notron lần lượt là l,0073u và l,0087u; 1u = 931,5 MeV/c2. Năng lượng liên kết của hạt nhân \(_5^{11}B\) là
Năng lượng liên kết của hạt nhân \(B\) là:
\(\begin{array}{l}{{\rm{W}}_{lk}} = \left[ {Z.{m_p} + \left( {A - Z} \right){m_n} - {m_X}} \right]{c^2}\\\,\,\,\,\,\,\,\,\, = \left[ {5.1,0073u + \left( {11 - 5} \right).1,0087u - 11,0066u} \right]{c^2} = 0,0821u{c^2} = 76,476MeV\end{array}\)
Bản chất lực tương tác giữa các nuclon trong hạt nhân là:
Lực tương tác giữa các nuclon gọi là lực hạt nhân (tương tác hạt nhân hay tương tác mạnh)
Phạm vi của lực tương tác mạnh trong hạt nhân là bao nhiêu?
Lực hạt nhân chỉ phát huy tác dụng trong phạm vi kích thước hạt nhân (khoảng 10-15 m)
Độ hụt khối của hạt nhân được xác định bằng biểu thức
Độ hụt khối của hạt nhân được xác định bằng biểu thức: \(\Delta m = Z{m_p} + \left( {A - Z} \right){m_n} - {m_X}\)
Xét đồng vị Côban \(_{27}^{60}Co\) hạt nhân có khối lượng mCo = 59,934u. Biết khối lượng của các hạt: mp = 1,007276u, mn = 1,008665u. Độ hụt khối của hạt nhân đó
Hạt nhân \(_{27}^{60}Co\) có: \(\left\{ \begin{array}{l}Z = 27\\N = A - Z = 60 - 27 = 33\end{array} \right.\)
Độ hụt khối của hạt nhân: \(_{27}^{60}Co\) là:
\(\Delta m = Z{m_p} + \left( {A - Z} \right){m_n} - {m_{Co}} = 27.1,007276 + 33.1,008665 - 59,934 = 0,548u\)

