Bài tập đồ thị dao động cơ nâng cao

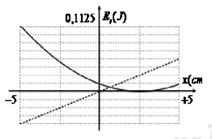
Từ đồ thị ta thấy khi thế năng đàn hồi bằng 0:

\({E_{tdh}} = 0 \Rightarrow \Delta {l_0} = 0 \Leftrightarrow x =  + 2,5\,\,cm\) → ở vị trí lò xo không biến dạng, li độ của vật: x = 2,5 cm

Vậy tại vị trí cân bằng, lò xo giãn một đoạn 2,5 cm, thế năng đàn hồi của vật khi đó:

\({E_{tdh}} = \dfrac{1}{2}k{x^2} \Leftrightarrow \dfrac{9}{{640}} = \dfrac{1}{2}k.0,{025^2} \Rightarrow k = 45\,\,\left( {N/m} \right)\)

Từ đồ thị ta thấy thế năng hấp dẫn cực đại của vật là:

\({E_{thd\max }} = mgA \Leftrightarrow \dfrac{9}{{160}} = m.10.0,05 \Rightarrow m = 0,1125\,\,\left( {kg} \right)\)

Tần số góc của con lắc là: \(\omega  = \sqrt {\dfrac{k}{m}}  = \sqrt {\dfrac{{45}}{{0,1125}}}  = 20\,\,\left( {rad/s} \right)\)

Ta có công thức độc lập với thời gian:

\({x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = {A^2} \Rightarrow 2,{5^2} + \dfrac{{{v^2}}}{{{{20}^2}}} = {5^2} \Rightarrow v = 86,6\,\,\left( {cm/s} \right)\)

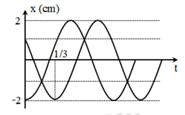
Từ đồ thị, ta thấy biên độ của hai dao động là: \({A_1} = {A_2} = 2\,\,\left( {cm} \right)\)

Ở thời điểm t = 0, li độ của dao động thứ nhất ở biên âm → pha ban đầu là: \({\varphi _1} = \pi \,\,\left( {rad} \right)\)

Ở thời điểm t = 0, li độ của dao động thứ hai là: \({x_{02}} = 1\,\,\left( {cm} \right) = \dfrac{{{A_2}}}{2}\)

Ở thời điểm \(t = \dfrac{1}{3}\,\,\left( s \right)\), li độ của dao động thứ hai là: \({x_2} =  - {A_2}\)

Ta có vòng tròn lượng giác:

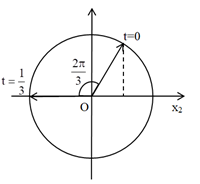
Từ vòng tròn lượng giác, ta thấy pha ban đầu của dao động thứ hai là: \({\varphi _2} = \dfrac{\pi }{3}\,\,\left( {rad} \right)\)

Trong khoảng thời gian từ t = 0 đến \(t = \dfrac{1}{3}\,\,\left( s \right)\), vecto \(\overrightarrow {{A_2}} \) quay được góc: \(\Delta \varphi  = \dfrac{{2\pi }}{3}\,\,\left( {rad} \right)\)

Tần số góc của dao động là: \({\omega _2} = {\omega _1} = \omega  = \dfrac{{\Delta \varphi }}{{\Delta t}} = \dfrac{{\dfrac{{2\pi }}{3}}}{{\dfrac{1}{3}}} = 2\pi \,\,\left( {rad/s} \right)\)

Phương trình hai dao động thành phần là:

\(\left\{ \begin{array}{l}{x_1} = 2\cos \left( {2\pi t + \pi } \right)\,\,\left( {cm} \right)\\{x_2} = 2\cos \left( {2\pi t + \dfrac{\pi }{3}} \right)\,\,\left( {cm} \right)\end{array} \right.\)

Sử dụng máy tính bỏ túi, ta có dao động tổng hợp:

\(x = {x_1} + {x_2} = 2\angle  - \pi  + 2\angle \dfrac{\pi }{3} = 2\angle \dfrac{{2\pi }}{3} \Rightarrow \left\{ \begin{array}{l}A = 2\,\,\left( {cm} \right)\\\varphi  = \dfrac{{2\pi }}{3}\,\,\left( {rad} \right)\end{array} \right.\)

Phương trình dao động tổng hợp là: \(x = 2\cos \left( {2\pi t + \dfrac{{2\pi }}{3}} \right)\,\,\left( {cm} \right)\)

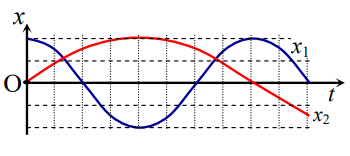
Từ đồ thị ta thấy hai chất điểm có biên độ bằng nhau và bằng A

Chu kì dao động của chất điểm thứ 2: \({T_2} = 2{T_1} \Rightarrow {\omega _2} = \frac{{{\omega _1}}}{2}\)

Hai chất điểm có cùng li độ x₁ = x₂, ta có:

\(\frac{{{{\rm{W}}_{d2}}}}{{{{\rm{W}}_{d1}}}} = \frac{{\frac{1}{2}m{\omega _2}^2\left( {{A^2} - {x_2}^2} \right)}}{{\frac{1}{2}m{\omega _1}^2\left( {{A^2} - {x_1}^2} \right)}} = \frac{{{\omega _2}^2}}{{{\omega _1}^2}} = \frac{1}{4} = 0,25\)

Từ đồ thị ta có:

Với đường (1):

\(\left\{ \begin{array}{l}{A_1} = 2cm\\{F_{k{v_1}ma{\rm{x}}}} = 2N = {k_1}{{\rm{A}}_1}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{A_1} = 2cm\\{k_1} = 100N/m\end{array} \right.\)

Với đường (2):

\(\left\{ \begin{array}{l}{A_2} = 1cm\\{F_{k{v_{2ma{\rm{x}}}}}} = 3N = {k_2}{A_2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{A_2} = 1cm\\{k_2} = 300N/m\end{array} \right.\)

Tại thời điểm \({t_1}\): \({x_1} = {x_2} = {A_2} = 1cm\)

Tại thời điểm \({t_2}\): khoảng cách giữa 2 vật nặng theo phương Ox là lớn nhất khi vuông góc với phương thẳng đứng, vẽ trên vòng tròn lượng giác ta được  vị trí của 2 vật: \(\left\{ \begin{array}{l}{x_1} = \frac{{{A_1}\sqrt 3 }}{2}\\{x_2} = 0\end{array} \right.\)

Khi đó:

Thế năng của con lắc 1 tại thời điểm \({t_2}\):

\({{\rm{W}}_{{t_1}}} = \frac{1}{2}{k_1}x_1^2 = \frac{1}{2}100.{\left( {\frac{{\sqrt 3 }}{2}.0,02} \right)^2} = 0,015J\)

Động năng của con lắc 2 tại thời điểm \({t_2}\):

\({{\rm{W}}_{{d_2}}} = {{\rm{W}}_2} = \frac{1}{2}{k_2}A_2^2 = \frac{1}{2}.300.0,{01^2} = 0,015J\)

\( \Rightarrow \frac{{{{\rm{W}}_{{t_1}}}}}{{{{\rm{W}}_{{d_2}}}}} = \frac{{0,015}}{{0,015}} = 1\)

Từ đồ thị, ta có biên độ:

A₁ = 5ô ; A₂  = 4ô

Xét lúc 2 dao động cùng có li độ: x₁ = x₂ = 2 ô.

Dùng vòng tròn lượng giác:

Độ lệch pha của 2 dao động:

\(\Delta \varphi  = {\alpha _1} + {\alpha _2} = {\cos ^{ - 1}}(\frac{2}{5}) + {\cos ^{ - 1}}(\frac{2}{4}) = 1.159 + \frac{\pi }{3} = 1.159 + 1,107 = 2,206\;rad\)

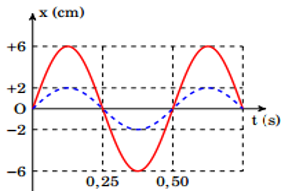
Từ đồ thị ta có:

+ Chu kì: \(T = 0,5s \Rightarrow \omega = \frac{{2\pi }}{T} = 4\pi \,\left( {rad/s} \right)\)

+ Biên độ dao động:\({A_1} = 6cm;{A_2} = 2cm\)

\( \Rightarrow \) Phương trình dao động của hai con lắc lò xo:

\(\left\{ \begin{array}{l}{x_1} = 6.cos\left( {4\pi t - \frac{\pi }{2}} \right)cm\\{x_2} = 2.cos\left( {4\pi t - \frac{\pi }{2}} \right)cm\end{array} \right.\)

\( \Rightarrow \frac{{{x_1}}}{{{x_2}}} = \frac{{{A_1}}}{{{A_2}}} = 3 \Rightarrow \frac{{{W_{t1}}}}{{{W_{t2}}}} = \frac{{x_1^2}}{{x_2^2}} = \frac{{A_1^2}}{{A_2^2}} = 9\)

Ở thời điểm t ta có:

\(\frac{{{W_{t1}}}}{{{W_{t2}}}} = \frac{{{W_1} - {W_{d1}}}}{{{W_{t2}}}} = 9 \Leftrightarrow \frac{{\frac{1}{2}m.{\omega ^2}A_1^2 - \frac{1}{2}mv_1^2}}{{{W_{t2}}}} = 9\)

\( \Leftrightarrow \frac{{\frac{1}{2}.m.{{\left( {4\pi } \right)}^2}.0,{{06}^2} - \frac{1}{2}.m.0,{{72}^2}}}{{{{4.10}^{ - 3}}}} = 9\)

\( \Rightarrow m = 1,25kg = \frac{5}{4}kg\)