Câu hỏi:
2 năm trước
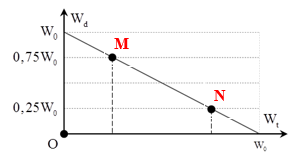
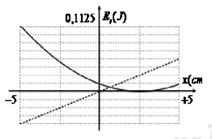
Một con lắc lò xo có đầu trên treo vào một điểm cố định, đầu dưới gắn vào một vật nặng dao động điều hòa theo phương thẳng đứng. Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của thế năng hấp dẫn và thế năng đàn hồi vào li độ x. Tốc độ của vật nhỏ khi đi qua vị trí lò xo không biến dạng bằng.
Trả lời bởi giáo viên
Đáp án đúng: c
Từ đồ thị ta thấy khi thế năng đàn hồi bằng 0:
\({E_{tdh}} = 0 \Rightarrow \Delta {l_0} = 0 \Leftrightarrow x = + 2,5\,\,cm\) → ở vị trí lò xo không biến dạng, li độ của vật: x = 2,5 cm
Vậy tại vị trí cân bằng, lò xo giãn một đoạn 2,5 cm, thế năng đàn hồi của vật khi đó:
\({E_{tdh}} = \dfrac{1}{2}k{x^2} \Leftrightarrow \dfrac{9}{{640}} = \dfrac{1}{2}k.0,{025^2} \Rightarrow k = 45\,\,\left( {N/m} \right)\)
Từ đồ thị ta thấy thế năng hấp dẫn cực đại của vật là:
\({E_{thd\max }} = mgA \Leftrightarrow \dfrac{9}{{160}} = m.10.0,05 \Rightarrow m = 0,1125\,\,\left( {kg} \right)\)
Tần số góc của con lắc là: \(\omega = \sqrt {\dfrac{k}{m}} = \sqrt {\dfrac{{45}}{{0,1125}}} = 20\,\,\left( {rad/s} \right)\)
Ta có công thức độc lập với thời gian:
\({x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = {A^2} \Rightarrow 2,{5^2} + \dfrac{{{v^2}}}{{{{20}^2}}} = {5^2} \Rightarrow v = 86,6\,\,\left( {cm/s} \right)\)
Hướng dẫn giải:
Thế năng hấp dẫn: \({E_{thd}} = mgz\)
Thế năng đàn hồi: \({E_{tdh}} = \dfrac{1}{2}k\Delta {l^2}\)
Công thức độc lập với thời gian: \({x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = {A^2}\)
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
