Câu hỏi:
2 năm trước
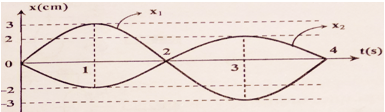
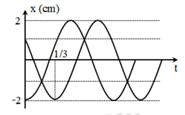
Đồ thị của hai dao động điều hòa cùng tần số được vẽ như sau. Phương trình dao động tổng hợp là
Trả lời bởi giáo viên
Đáp án đúng: a
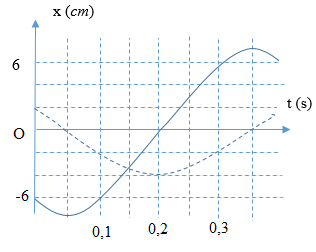
Từ đồ thị, ta thấy biên độ của hai dao động là: \({A_1} = {A_2} = 2\,\,\left( {cm} \right)\)
Ở thời điểm t = 0, li độ của dao động thứ nhất ở biên âm → pha ban đầu là: \({\varphi _1} = \pi \,\,\left( {rad} \right)\)
Ở thời điểm t = 0, li độ của dao động thứ hai là: \({x_{02}} = 1\,\,\left( {cm} \right) = \dfrac{{{A_2}}}{2}\)
Ở thời điểm \(t = \dfrac{1}{3}\,\,\left( s \right)\), li độ của dao động thứ hai là: \({x_2} = - {A_2}\)
Ta có vòng tròn lượng giác:
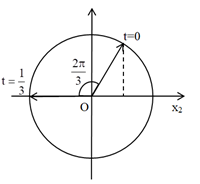
Từ vòng tròn lượng giác, ta thấy pha ban đầu của dao động thứ hai là: \({\varphi _2} = \dfrac{\pi }{3}\,\,\left( {rad} \right)\)
Trong khoảng thời gian từ t = 0 đến \(t = \dfrac{1}{3}\,\,\left( s \right)\), vecto \(\overrightarrow {{A_2}} \) quay được góc: \(\Delta \varphi = \dfrac{{2\pi }}{3}\,\,\left( {rad} \right)\)
Tần số góc của dao động là: \({\omega _2} = {\omega _1} = \omega = \dfrac{{\Delta \varphi }}{{\Delta t}} = \dfrac{{\dfrac{{2\pi }}{3}}}{{\dfrac{1}{3}}} = 2\pi \,\,\left( {rad/s} \right)\)
Phương trình hai dao động thành phần là:
\(\left\{ \begin{array}{l}{x_1} = 2\cos \left( {2\pi t + \pi } \right)\,\,\left( {cm} \right)\\{x_2} = 2\cos \left( {2\pi t + \dfrac{\pi }{3}} \right)\,\,\left( {cm} \right)\end{array} \right.\)
Sử dụng máy tính bỏ túi, ta có dao động tổng hợp:
\(x = {x_1} + {x_2} = 2\angle - \pi + 2\angle \dfrac{\pi }{3} = 2\angle \dfrac{{2\pi }}{3} \Rightarrow \left\{ \begin{array}{l}A = 2\,\,\left( {cm} \right)\\\varphi = \dfrac{{2\pi }}{3}\,\,\left( {rad} \right)\end{array} \right.\)
Phương trình dao động tổng hợp là: \(x = 2\cos \left( {2\pi t + \dfrac{{2\pi }}{3}} \right)\,\,\left( {cm} \right)\)
Hướng dẫn giải:
Sử dụng kĩ năng đọc đồ thị
Sử dụng vòng tròn lượng giác và công thức: \(\omega = \dfrac{{\Delta \varphi }}{{\Delta t}}\)
Viết phương trình dao động thành phần
Sử dụng máy tính bỏ túi để tìm dao động tổng hợp
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
