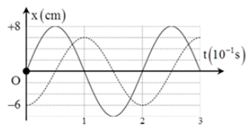
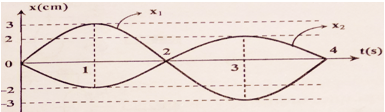
Một vật thực hiện 2 dao động điều hòa cùng phương, cùng tần số có đồ thị như hình vẽ. Đồ thị x1 (t) là đường nét liền, đồ thị x2 (t) là đường nét đứt. Trong 0,8 s đầu tiên kể từ t = 0s, tốc độ trung bình của vật là:
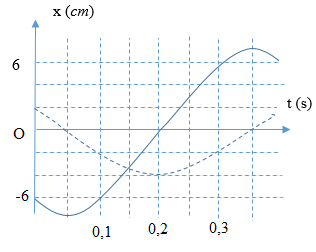
Trả lời bởi giáo viên
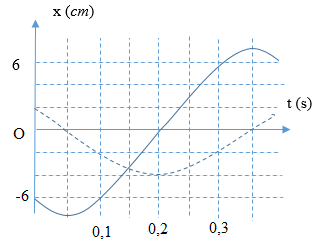
Từ đồ thị ta xác định được chu kì dao động của hai dao động:
\(T = 0,6s \Rightarrow \omega = \frac{{2\pi }}{T} = \frac{{10\pi }}{3}\left( {rad/s} \right)\)
Dao động x1 sau 0,2s thì vật có li độ bằng 0 lần thứ nhất. Ta có :
\(\omega .t + {\varphi _{01}} = \frac{{ - \pi }}{2} \Rightarrow \frac{{10\pi }}{3}.0,2 + {\varphi _{01}} = \frac{{ - \pi }}{2} \Rightarrow {\varphi _{01}} = \frac{{ - \pi }}{2} - \frac{{2\pi }}{3} = \frac{{ - 7}}{6}\pi \)
Pha ban đầu của dao động x1là :
\({\varphi _{01}} = \frac{{ - 7\pi }}{6}\)
Biên độ dao động của x1là :
\(A = \frac{{ - 6}}{{\cos \frac{{ - 7\pi }}{6}}} = 4\sqrt 3 \left( {cm} \right)\)
Vậy phương trình dao động 1:
\({x_1} = 4\sqrt 3 .\cos \left( {\frac{{10\pi }}{3}t - \frac{{7\pi }}{6}} \right)cm\)
Dao động x2 tại t = 0 thì vật có li độ bằng 2. Ta có:
\(\cos {\varphi _{02}} = \frac{{{x_2}}}{{{A_2}}} = \frac{2}{4} \Rightarrow {\varphi _{02}} = \frac{\pi }{3}\)
Pha ban đầu của dao động x2là:
\({\varphi _{02}} = \frac{\pi }{3}\)
Biên độ dao động của x2 là A2 = 4 cm.
Vậy phương trình dao động 2: \({x_2} = 4.\cos \left( {\frac{{10\pi }}{3}t + \frac{\pi }{3}} \right)cm\)
Dao động tổng hợp là :
\(x = {x_1} + {x_2} = 8.\cos \left( {\frac{{10\pi }}{3}.t + \frac{{2\pi }}{3}} \right)cm\)
Ta có:
\(0,8s = 0,6s\; + 0,2s = T + \frac{T}{3}\)
Vậy quãng đường vật đi được sau thời gian 0,8 s là :
\(S = 4A + \Delta S\)
Với ∆S là quãng đường đi được trong 1/3 chu kì.
Tại thời điểm ban đầu vật có vị trí:
\({x_0} = 8.\cos \frac{{2\pi }}{3} = - 4cm\)
Sau \(\frac{T}{3}\) vật đến vị trí \(x = 8.\cos \left( {\frac{{4\pi }}{3}} \right) = - 4cm\)
Quãng đường vật đi được trong thời gian \(\frac{T}{3}\) này là ∆S = 8cm
Vậy quãng đường vật đi được sau thời gian 0,8 s là :
\(\;S = 4A + \Delta S = 4.8 + 8 = 40cm\)
Vận tốc trung bình trong thời gian này là:
\(v = \frac{{40}}{{0,8}} = 50\left( {cm/s} \right)\)
Hướng dẫn giải:
Phương trình dao động điều hòa tổng quát là \(x = A.\cos \left( {\omega t + \varphi } \right)\).
Từ đồ thị ta xác định được chu kì dao động của hai dao động, biên độ dao động và viết được hai phương trình dao động, sau đó tổng hợp hai dao động: x = x1 + x2
Sau đó tìm quãng đường mà vật đi được trong 0,8s đầu tiên và tính vận tốc trung bình:
\({v_{tb}} = \frac{S}{t}\)