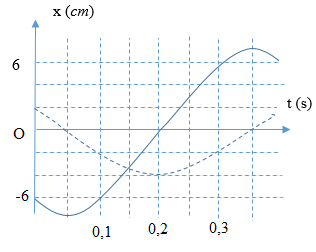
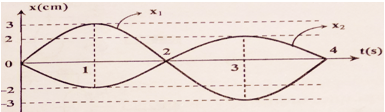
Chất điểm tham gia đồng thời hai dao động điều hoà cùng phương có đồ thị như hình vẽ. Phương trình dao động tổng hợp của chất điểm là:

Một vật thực hiện 2 dao động điều hòa cùng phương, cùng tần số có đồ thị như hình vẽ. Đồ thị x₁ (t) là đường nét liền, đồ thị x₂ (t) là đường nét đứt. Trong 0,8 s đầu tiên kể từ t = 0s, tốc độ trung bình của vật là:

Một con lắc lò xo gồm một vật nhỏ có khối lượng \(200 g\) và lò xo có độ cứng \(k\), đang dao động điều hòa theo phương thẳng đứng. Chọn gốc tọa độ ở vị trí cân bằng, chiều dương hướng xuống. Hình trên là đồ thị biểu diễn sự phụ thuộc của lực đàn hồi \(F\) tác dụng lên vật theo thời gian \(t\). Biết \({F_1} + 3{F_2} + 6{F_3} = 0\). Lấy \(g =10 m/s^2\). Tại \(t = 0\), độ lớn của lực đàn hồi tác dụng lên vật có giá trị gần nhất với giá trị nào sau đây ? 

Khảo sát thực nghiệm một con lắc lò xo gồm vật nhỏ có khối lượng \(216{\rm{ }}g\) và lò xo có độ cứng k, dao động dưới tác dụng của ngoại lực \(F{\rm{ }} = {\rm{ }}{F_0}cos2\pi ft\), với \({F_0}\) không đổi và \(f\) thay đổi được. Kết quả khảo sát ta được đường biểu diễn biên độ \(A\) của con lắc theo tần số \(f\) có đồ thị như hình vẽ. Giá trị của \(k\) xấp xỉ bằng:

Đồ thị biểu diễn mối quan hệ giữa động năng \({W_d}\) và thế năng \({W_t}\) của một vật dao động điều hòa có cơ năng \({W_0}\) như hình vẽ. Ở thời điểm t nào đó, trạng thái năng lượng của dao động có vị trí M trên đồ thị, lúc này vật đang có li độ dao động \(x{\rm{ }} = {\rm{ }}2{\rm{ }}cm\). Biết chu kỳ biến thiên của động năng theo thời gian là \({T_d} = {\rm{ }}0,5{\rm{ }}s\), khi vật có trạng thái năng lượng ở vị trí N trên đồ thị thì vật dao động có tốc độ là:

Hai dao động điều hòa có đồ thị li độ - thời gian như hình vẽ. Tổng vận tốc tức thời của hai dao động có giá trị lớn nhất là

Một con lắc lò xo đang dao động điều hòa, lực đàn hồi của lò xo phụ thuộc vào chiều dài của lò xo như đồ thị hình vẽ. Cho \(g{\rm{ }} = {\rm{ }}10{\rm{ }}m/{s^2}\). Biên độ và chu kì dao động của con lắc là