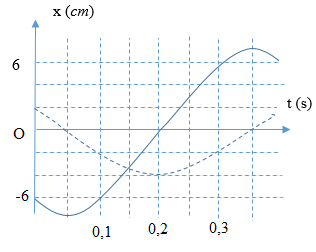
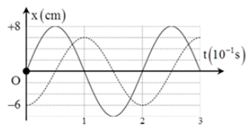
Hai dao động điều hòa có đồ thị li độ - thời gian như hình vẽ. Tổng vận tốc tức thời của hai dao động có giá trị lớn nhất là
Trả lời bởi giáo viên
+ Từ đồ thị, ta có \(\left\{ \begin{array}{l}{A_1} = 8cm\\{A_2} = 6cm\end{array} \right.\,\), $T = {2.10^{ - 1}}s \to \omega = \dfrac{{2\pi }}{T} = 10\pi rad/s$ và hai dao động vuông pha (do tại \(t = 0\) một dao động đang ở biên âm và một dao động đang ở vị trí cân bằng)
=> Biên độ dao động tổng hợp của hai dao động: $A = \sqrt {A_1^2 + A_2^2} $
$ \to $ Tổng vận tốc tức thời cực đại: ${v_{max}} = \omega A = \omega \sqrt {A_1^2 + A_2^2} = 10\pi \sqrt {{6^2} + {8^2}} = 100\pi cm/s$
Hướng dẫn giải:
+ Sử dụng biểu thức tính biên độ dao động tổng hợp của hai dao động: \({A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}{\rm{cos}}\Delta \varphi \)
+ Vận tốc cực đại: \({v_{\max }} = \omega A\)