Câu hỏi:
2 năm trước
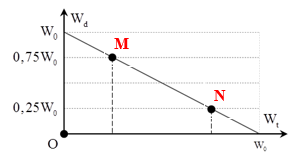
Đồ thị biểu diễn mối quan hệ giữa động năng \({W_d}\) và thế năng \({W_t}\) của một vật dao động điều hòa có cơ năng \({W_0}\) như hình vẽ. Ở thời điểm t nào đó, trạng thái năng lượng của dao động có vị trí M trên đồ thị, lúc này vật đang có li độ dao động \(x{\rm{ }} = {\rm{ }}2{\rm{ }}cm\). Biết chu kỳ biến thiên của động năng theo thời gian là \({T_d} = {\rm{ }}0,5{\rm{ }}s\), khi vật có trạng thái năng lượng ở vị trí N trên đồ thị thì vật dao động có tốc độ là:
Trả lời bởi giáo viên
Đáp án đúng: c
+ Chu kì biến thiên của động năng là: \(T' = 0,5s = \dfrac{T}{2} \to T = 1s\)
+ Tần số góc của dao động: \(\omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{1} = 2\pi rad/s\)
Từ đồ thị, xét tại các vị trí:
- Vị trí M, có:
$\begin{array}{l}{{\rm{W}}_{{d_M}}} = 0,75{W_0}\\ \to {{\rm{W}}_{{t_M}}} = {{\rm{W}}_0} - {{\rm{W}}_{{d_M}}} = {{\rm{W}}_0} - 0,75{W_0} = 0,25{W_0}\end{array}$
$\begin{array}{l}{{\rm{W}}_{{t_M}}} = 0,25{W_0} \leftrightarrow \dfrac{1}{2}kx_M^2 = 0,25.\dfrac{1}{2}k{A^2}\\ \to {x_M} = \dfrac{A}{2}\end{array}$
Theo đầu bài, ta có: \({x_M} = 2cm = \dfrac{A}{2} \to A = 4cm\)
- Vị trí N, có:
$\begin{array}{l}{{\rm{W}}_{{d_N}}} = 0,25{W_0}\\ \to {{\rm{W}}_{{t_N}}} = {{\rm{W}}_0} - {{\rm{W}}_{{d_N}}} = {{\rm{W}}_0} - 0,25{W_0} = 0,75{W_0}\end{array}$
$\begin{array}{l}{{\rm{W}}_{{t_N}}} = 0,75{W_0} \leftrightarrow \dfrac{1}{2}kx_N^2 = 0,75\dfrac{1}{2}k{A^2}\\ \to x_N^2 = 0,75{A^2}\end{array}$
+ Áp dụng hệ thức độc lập ta có:
\(\begin{array}{l}{A^2} = x_N^2 + \dfrac{{{v^2}}}{{{\omega ^2}}} \leftrightarrow {A^2} = 0,75{A^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}\\ \to {v^2} = 0,25{A^2}{\omega ^2}\\ \to v = 0,5.A\omega = 0,5.4.2\pi = 4\pi cm/s\end{array}\)
Hướng dẫn giải:
+ Đọc đồ thị
+ Chu kì biến thiên của động năng: \(T' = \dfrac{T}{2}\)
+ Sử dụng biểu thức tính tần số góc \(\omega = \dfrac{{2\pi }}{T}\)
+ Xét động năng, thế năng tại các vị trí
+ Áp dụng biểu thức tính cơ năng: ${\rm{W}} = {{\rm{W}}_t} + {{\rm{W}}_d} = \dfrac{1}{2}k{x^2} + \dfrac{1}{2}m{v^2} = \dfrac{1}{2}k{A^2}$
+ Sử dụng hệ thức độc lập: \({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}\)
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
