Một vật dao động điều hòa có phương trình \(x = 5cos(2\pi t)\). Vận tốc của vật khi có li độ $x=3 cm$ là:
Ta có: ${A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}{\text{ }} \to {\text{v = }} \pm \omega \sqrt {{A^2} - {x^2}} $
Thay \(A = 5cm,{\rm{ }}x = 3cm\), tần số góc: \(\omega = 2\pi \left( {rad/s} \right)\) $ \to {\text{v}} = \pm 2\pi \sqrt {{5^2} - {3^2}} = \pm 8\pi cm/s \approx \pm 25,12cm/s$
Một vật dao động điều hòa có phương trình \(x = 5cos(2\pi t - \frac{\pi }{6})cm\). Lấy \({\pi ^2} = 10\). Gia tốc của vật khi có li độ $x= 3 cm$ là:
Ta có: \(a = - {\omega ^2}x\)
=> Tại \(x = 3cm{\rm{ }} = > a = - {(2\pi )^2}.3 = - 12{\pi ^2} = - 120cm/{s^2}\)
Một vật dao động điều hoà với phương trình \(x = {\rm{ }}Acos(\omega t{\rm{ }} + \varphi )\), tại thời điểm $t = 0$ thì li độ $x=A$. Pha ban đầu của dao động là:
Ta có: tại \(t = 0,{\rm{ }}x = Acos\varphi = A \to cos\varphi = 1 \to \varphi = 0\)
Dao động điều hoà có vận tốc cực đại là \({v_{max}} = 8\pi cm/s\) và gia tốc cực đại \({a_{max}} = 16{\pi ^2}cm/{s^2}\) thì tần số của dao động là:
Ta có: $\left\{ \begin{gathered}{v_{{\text{max}}}} = \omega A \hfill \\{a_{{\text{max}}}} ={\omega ^2}A \hfill \\\end{gathered} \right. \to \left[ {\dfrac{{{a_{{\text{max}}}}}}{{{v_{{\text{max}}}}}} = \dfrac{{{\omega ^2}A}}{{\omega A}} = \omega = \dfrac{{16{\pi ^2}}}{{8\pi }} = 2\pi = 2\pi f \to f = \dfrac{\omega }{{2\pi }}} \right. = 1H{\text{z}}$
Dao động điều hoà có vận tốc cực đại là \({v_{max}} = 16\pi cm/s\) và gia tốc cực đại \({a_{max}} = 64{\pi ^2}cm/{s^2}\) thì biên độ của dao động là:
Ta có: $\left\{ \begin{gathered}{v_{{\text{max}}}} = \omega A \hfill \\{a_{{\text{max}}}} = {\omega ^2}A \hfill \\\end{gathered} \right. \to \dfrac{{{v^2}_{{\text{max}}}}}{{{a_{{\text{max}}}}}} = \dfrac{{{{(\omega A)}^2}}}{{{\omega ^2}A}} = A = \dfrac{{{{\left( {16\pi } \right)}^2}}}{{64\pi^2 }} = 4cm$
Một chất điểm dao động điều hoà với phương trình dạng\(x=cos(2\pi t + \dfrac{\pi}{6})(cm,s)\). Lấy \(\pi ^2 =10\), biểu thức gia tốc tức thời của chất điểm là:
Ta có: $a = - {\omega ^2}Acos(\omega t + \varphi ) = {\omega ^2}Acos(\omega t + \varphi + \pi )$
x = cos(2πt + π/6) (cm, s) $ \to a = - {(2\pi )^2}.1cos(2\pi t + \dfrac{\pi }{6}) = - 40cos(2\pi t + \dfrac{\pi }{6})$
Một vật thực hiện dao động điều hòa trên đoạn thẳng dài 12cm. Thời gian để vật đi được đoạn đường dài 24cm là 2s. Tốc độ của vật khi đi qua vị trí cân bằng là
Ta có: \(A = \dfrac{L}{2} = \dfrac{{12}}{2} = 6cm\)
Vật đi được quãng đường \(S = 24cm = 4.A\) trong 2s \( \Rightarrow T = 2s\)
→ Tốc độ của vật khi qua vị trí cân bằng \({v_{ma{\rm{x}}}} = \omega A = 6\pi \,\,\left( {cm/s} \right)\)
Một điểm M chuyển động tròn đều trên một đường tròn với tốc độ 15 cm/s. Gọi P là hình chiếu của M lên một đường kính của đường tròn quỹ đạo. Tốc độ trung bình của P trong một dao động toàn phần bằng
Tốc độ dài của chuyển động tròn đều: \({v_M} = 15\,\,cm/s = \omega R = \omega A = {v_{\max }} = {v_P}\)
Tốc độ trung bình trong 1 chu kì: \(\overline v = \dfrac{S}{t} = \dfrac{{4A}}{T} = \dfrac{{4A\omega }}{{2\pi }} = \dfrac{{2A\omega }}{\pi }\)
\( \Rightarrow \overline v = \dfrac{{2{v_{\max }}}}{\pi } = \dfrac{{2{v_p}}}{\pi } = \dfrac{{2.15}}{\pi } = 9,55\,\,\left( {cm/s} \right)\)
Một vật dao động điều hòa có đồ thị biểu diễn li độ x theo thời gian t như hình bên. Chu kì dao động của vật là
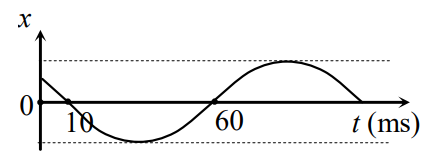
Từ đồ thị ta thấy trong khoảng thời gian từ 10 ms đến 60 ms, vật thực hiện được \(\frac{1}{2}\) chu kì:
\(\frac{T}{2} = 60 - 10 \Rightarrow T = 100\,\,\left( {ms} \right) = 0,1\,\,\left( s \right)\)
Đề thi thử THPT chuyên Lam Sơn - 2021
Một chất điểm dao động theo phương trình \(x = 6co{\rm{s}}\omega {\rm{t}}\left( {cm} \right)\). Dao động của chất điểm có biên độ là
Phương trình dao động: \(x = 6cos\omega t\left( {cm} \right)\)
\( \Rightarrow \) Biên độ dao động \(A = 6cm\)

