Xét phản ứng: $_1^2{\text{H}} + _1^2{\text{H}} \to {\text{ }}_2^3{\text{He}} + _0^1{\text{n}}$. Xác định năng lượng tỏa ra bởi phản ứng đó (tính ra MeV và ra J). Cho biết khối lượng của các hạt nhân $_1^2{\text{H;}}_2^3{\text{He}};_0^1{\text{n}}$ lần lượt là: 2,0135 u; 3,0149 u ; 1,0087 u
Đáp án A
Cách giải:
a) Xét phản ứng: $_1^2{\text{H}} + _1^2{\text{H}} \to {\text{ }}_2^3{\text{He}} + {\text{ }}_0^1{\text{n}}$
Năng lượng toả ra bởi phản ứng:
$\eqalign{
& {W_{toa}}\; = \left( {{m_H} + {m_H} - {m_{He}} - {m_n}} \right){{\rm{c}}^2}{\rm{ = }}\left( {2,0135u + 2,0135u - 3,0149u - 1,0087u} \right){{\rm{c}}^2} \cr
& {{\rm{W}}_{toa}}{\rm{ = 3}},{\rm{4}}.{\rm{1}}{{\rm{0}}^{ - 3}}.931,5MeV = {\rm{3}},1671MeV = 3,1671.1,{6.10^{ - 13}}\;J \approx 5,{07.10^{ - 13}}J \cr} $
Cho phản ứng tổng hợp hạt nhân $2{}_{1}^{2}D\to {}_{Z}^{A}X+{}_{0}^{1}n$. Biết độ hụt khối của hạt nhân ${}_{1}^{2}D$ là 0,0024u, của hạt nhân X là 0,0083u. Lấy 1u = 931 MeV/c2. Năng lượng toả ra khi tổng hợp hết 1g ${}_{1}^{2}D$ là
Nhận xét: mỗi phương trình sử dụng 2 hạt nhân D
Năng lượng toả ra của một phản ứng là:
E = (−2ΔmD + mX).c2 = (−2.0,0024 + 0,0083).931 = 3,2585 MeV
1g D có số hạt nhân D là: $N=\frac{1}{2}{{N}_{A}}$
Vậy phản ứng tổng hợp hết 1g D thì năng lượng tỏa ra là:
$\sum{E}=E.\frac{N}{2}=3,2585.\frac{0,5}{2}.6,{{023.10}^{23}}=4,{{906.10}^{23}}\,MeV$
Hạt nhân \(X\) bị phóng xạ tạo thành hạt nhân \(Y\). Ban đầu, có một mẫu chứa chất phóng xạ \(X\) nguyên chất, khi phân rã, số hạt nhân \(X\) còn lại \(N\) phụ thuộc vào thời gian \(t\) được mô tả như đồ thị hình bên. Tỉ số giữa số hạt nhân \(Y\) được sinh ra và số hạt nhân \(X\) còn lại trong mẫu ở thời điểm \({t_2}\) là
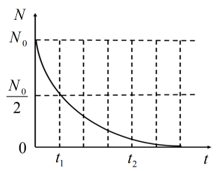
Từ đồ thị ta thấy tại thời điểm \({t_1}\), số hạt nhân \(X\) còn lại là:
\(N = \dfrac{{{N_0}}}{2} \Rightarrow {N_0}{.2^{ - \dfrac{{{t_1}}}{T}}} = \dfrac{{{N_0}}}{2} \Rightarrow {t_1} = T\)
Ở thời điểm \({t_2} = 4{t_1} = 4T\), tỉ số hạt \(Y\) sinh ra và hạt \(X\) còn lại là:
\(\dfrac{{{N_Y}}}{{{N_X}}} = \dfrac{{{N_0}.\left( {1 - {2^{ - \dfrac{{{t_2}}}{T}}}} \right)}}{{{N_0}{{.2}^{ - \dfrac{{{t_2}}}{T}}}}} = \dfrac{{1 - {2^{ - 4}}}}{{{2^{ - 4}}}} = 15\)

