Năng lượng, vận tốc, lực của con lắc đơn
Kỳ thi ĐGTD ĐH Bách Khoa
Một con lắc đơn gồm vật có khối lượng 100g, chiều dài dây l = 40cm. Kéo vật lệch khỏi VTCB để dây treo hợp với phương thẳng đứng một góc 300 rồi buông tay. Lấy g = 10m/s2. Vận tốc của vật khi qua vị trí góc α=150 có độ lớn là:
Ta có, vận tốc của con lắc:
\({v_{{{15}^0}}} = \pm \sqrt {2gl(c{\rm{os}}\alpha {\rm{ - cos}}{\alpha _0})} = \pm \sqrt {2.10.0,4(c{\rm{os1}}{{\rm{5}}^0}{\rm{ - cos3}}{{\rm{0}}^0})} = \pm 0,894m/s\)
Một con lắc đơn dao động điều hòa tại một nơi có g = 10m/s2, chiều dài dây treo là l = 1,6m với biên độ góc \({\alpha _0}\) = 0,1rad/s thì khi đi qua vị trí có li độ góc \(\frac{{{\alpha _0}}}{2}\) vận tốc có độ lớn là:
Vận tốc của con lắc đơn dao động điều hòa:
\({v_{\frac{{{\alpha _0}}}{2}}} = \pm \sqrt {gl({\alpha _0}^2{\rm{ - }}{\alpha ^2})} = \pm \sqrt {10.1,6({\rm{0,}}{{\rm{1}}^2}{\rm{ - }}{{\left( {\frac{{0,1}}{2}} \right)}^2})} = \frac{{\sqrt 3 }}{5}m/s = 20\sqrt 3 cm/s\)
Con lắc đơn dao động nhỏ với chu kỳ $2s$ tại nơi có gia tốc rơi tự do \(g = {\pi ^2} = 10m/{s^2}\). Vận tốc của con lắc tại vị trí có li độ góc $3^0$ có độ lớn là $28,7cm/s$. Biên độ góc của dao động là:
+ Chu kì dao động:
\(T = 2\pi \sqrt {\dfrac{l}{g}} \to l = \dfrac{{{T^2}g}}{{4{\pi ^2}}} = \dfrac{{{2^2}.10}}{{4{\pi ^2}}} = 1m\)
Vận tốc của con lắc đơn dao động điều hòa:
\({v_\alpha } = \pm \sqrt {gl({\alpha _0}^2{\rm{ - }}{\alpha ^2})} \to {\alpha _0} = \pm \sqrt {\dfrac{{{v_\alpha }^2}}{{gl}} + {\alpha ^2}} = \pm \sqrt {\dfrac{{0,{{287}^2}}}{{10.1}} + {{\left( {\dfrac{{3\pi }}{{180}}} \right)}^2}} = 0,105ra{\rm{d}} = {6^0}\)
Một con lắc đơn gồm vật có khối lượng 100g, chiều dài dây l = 40cm. Kéo vật lệch khỏi VTCB để dây treo hợp với phương thẳng đứng một góc 300 rồi buông tay. Lấy g = 10m/s2. Lực căng của dây treo khi vật qua vị trí cao nhất là :
Lực căng dây treo khi vật qua vị trí cao nhất :
\(T = mg(3c{\rm{os}}{\alpha _0}{\rm{ - 2cos}}{\alpha _0}) = mg({\rm{cos}}{\alpha _0}) = 0,1.10.c{\rm{os3}}{{\rm{0}}^0} = \frac{{\sqrt 3 }}{2}N\)
Một con lắc đơn gồm vật nặng có khối lượng m dao động điều hòa với biên độ góc α0 nhỏ. Biểu thức tính lực căng dây ở li độ α là:
Biểu thức xác định lực căng dây tại vị trí α bất kì của con lắc đơn dao động tự do:
\(T = mg(1 - 1,5{\alpha ^2}{\rm{ + }}{\alpha _0}^2)\)
Một con lắc đơn dao động điều hòa với biên độ góc α0 có cosα0 = 0,97. Khi vật đi qua vị trí có li độ góc α thì lực căng dây bằng trọng lực của vật. Giá trị cosα bằng:
Ta có: lực căng dây được xác định bằng biểu thức:
\(\begin{array}{l}T = mg(3c{\rm{os}}\alpha {\rm{ - 2cos}}{\alpha _0}) = P = mg\\ \to 3c{\rm{os}}\alpha - {\rm{2cos}}{\alpha _0} = 1\\ \to c{\rm{os}}\alpha = \dfrac{{1 + 2c{\rm{os}}{\alpha _0}}}{3} = \dfrac{{1 + 2.0,97}}{3} = 0,98\end{array}\)
Một con lắc đơn đang dao động điều hòa với biên độ góc α0 tại nơi có gia tốc trọng trường là g. Biết lực căng dây lớn nhất bằng 1.02 lần lực căng dây nhỏ nhất. Giá trị của α0 là ?
Ta có:
+ lực căng dây cực đại tại vị trí α = 0:
\({T_{{\rm{max}}}} = mg(3{\rm{ - 2cos}}{\alpha _0})\)
+ lực căng dây cực tiểu tại vị trí α = α0:
\({T_{\min }} = mg.c{\rm{os}}{\alpha _0}\)
\( \to \frac{{{T_{{\rm{max}}}}}}{{{T_{\min }}}} = \frac{{3 - 2c{\rm{os}}{\alpha _0}}}{{{\rm{cos}}{\alpha _0}}} = 1,02 \to c{\rm{os}}{\alpha _0} = 0,993 \to {\alpha _0} = 6,{6^0}\)
Một con lắc đơn đang dao động điều hòa với biên độ góc bằng \(9^0\) dưới tác dụng của trọng lực. Ở thời điểm \(t_0\), vật nhỏ của con lắc có li độ góc và li độ cong lần lượt là \(4,5^0\) và \(2,5 \pi cm\). Lấy \(g = 10 m/s^2\). Tốc độ của vật ở thời điểm \(t_0\) bằng
Ta có:
\({\alpha _0} = {9^0} = \dfrac{{9\pi }}{{180}}rad\)
\(\alpha = 4,{5^0} = \dfrac{{4,5\pi }}{{180}}rad\)
Theo đề bài, ta có tại thời điểm \({t_0}\): \(\left\{ \begin{array}{l}s = 2,5\pi cm\\\alpha = \dfrac{{4,5\pi }}{{180}}rad\end{array} \right.\)
Lại có \(s = l\alpha \Rightarrow l = \dfrac{s}{\alpha } = \dfrac{{2,5\pi }}{{\dfrac{{4,5\pi }}{{180}}}} = 100cm = 1m\)
Ta có, vận tốc tại vị trí \(\alpha \) bất kì khi góc \( < {10^0}\): \(v = \sqrt {gl\left( {\alpha _0^2 - {\alpha ^2}} \right)} \)
Ta suy ra, vận tốc của vật tại thời điểm \({t_0}\) là: \(v = \sqrt {gl\left( {\alpha _0^2 - {\alpha ^2}} \right)} = \sqrt {10.1\left( {{{\left( {\dfrac{{9\pi }}{{180}}} \right)}^2} - {{\left( {\dfrac{{4,5\pi }}{{180}}} \right)}^2}} \right)} = 0,43m = 43cm\)
Một con lắc đơn dao động điều hòa với phương trình li độ dài: \(s = 2cos7t (cm)\) (t: giây), tại nơi có gia tốc trọng trường \(g = 9,8 (m/s^2)\). Tỷ số giữa lực căng dây và trọng lực tác dụng lên quả cầu ở vị trí cân bằng là:
Từ phương trình li độ dài của con lắc đơn: \(s = 2cos7t\)
Ta có: Tần số góc của dao động: \(ω =7 (rad/s)\)
Mặt khác:
\(\omega = \sqrt {\dfrac{g}{l}} = 7 \to l = \dfrac{g}{{{\omega ^2}}} = \dfrac{{9,8}}{{{7^2}}} = 0,2m\)
\(s_0= 2cm = 0,02m=l\alpha_0 \\\to \alpha_0= 0,1 rad = 5,73^0\)
+ Lực căng dây tại VTCB:
\(T = mg(3 - 2c{\rm{os}}{\alpha _0}) \approx 1,01mg\)
\( \to \dfrac{T}{P} = \dfrac{{1,01mg}}{{mg}} = 1,01\)
Một con lắc đơn đang dao động điều hòa với biên độ góc 5o. Khi vật nặng đi qua vị trí cân bằng thì người ta giữ chặt điểm chính giữa của dây treo, sau đó vật tiếp tục dao động điều hòa với biên độ góc α0. Giá trị của α0 bằng:
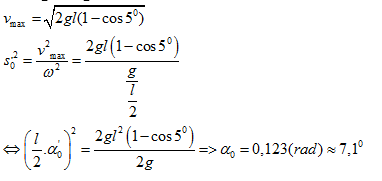
Con lắc đơn có khối lượng \(200g\) dao động với phương trình \(s = 10sin(2t) cm\). Ở thời điểm \(t = \dfrac{\pi }{6}s\), con lắc có động năng là:
Từ phương trình li độ dài: \(s = 10sin(2t)\)
Tại \(t = \dfrac{\pi }{6}s\), ta có
\(s = 10sin(2.\dfrac{\pi }{6}) = 5\sqrt 3 cm\)
Thế năng tại thời điểm đó:
\({{\rm{W}}_t} = \dfrac{1}{2}m{\omega ^2}{s^2} = \dfrac{1}{2}0,{2.2^2}{(5\sqrt 3 {.10^{ - 2}})^2} = {3.10^{ - 3}}J\)
Cơ năng của con lắc đơn:
\(W = \dfrac{1}{2}m{\omega ^2}{S_0}^2 = \dfrac{1}{2}0,{2.2^2}{({10.10^{ - 2}})^2} = {4.10^{ - 3}}J\)
=> Động năng của con lắc tại thời điểm đó:
\({{\rm{W}}_{\rm{d}}} = {\rm{W}} - {{\rm{W}}_t} = {4.10^{ - 3}} - {3.10^{ - 3}} = {10^{ - 3}}J\)
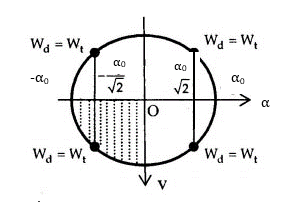
Tại nơi có gia tốc trọng trường g, một con lắc đơn dao động điều hòa với biên độ góc α0 nhỏ. Lấy mốc thế năng ở vị trí cân bằng, khi con lắc chuyển động nhanh dần theo chiều dương đến vị trí có động năng bằng thế năng thì li độ góc α của con lắc bằng:
Ta có: Thế năng và cơ năng của con lắc: \({{\rm{W}}_t} = \frac{1}{2}mgl{\alpha ^2};{{\rm{W}}_{\rm{d}}} = \frac{1}{2}mgl{\alpha _0}^2\)
Khi
\({{\rm{W}}_{\rm{d}}} = {{\rm{W}}_t} \to {\rm{W}} = {{\rm{W}}_{\rm{d}}} + {{\rm{W}}_t} = 2{{\rm{W}}_t} \leftrightarrow \frac{1}{2}mgl{\alpha _0}^2 = 2.\frac{1}{2}mgl{\alpha ^2} \to \alpha = \pm \frac{{{\alpha _0}}}{{\sqrt 2 }}\)
Con lắc chuyển động nhanh dần theo chiều dương khi con lắc chuyển động từ biên âm về VTCB theo chiều dương (vùng 3) => \(\alpha = - \frac{{{\alpha _0}}}{{\sqrt 2 }}\)
Một con lắc đơn có chiều dài 1 m, và vật có khối lượng 150 g, treo tại nơi có gia tốc trọng trường\(g = 10\,\,m/{s^2};\,\,{\pi ^2} = 10\). Tại vị trí cân bằng người ta truyền cho con lắc vận tốc \(\dfrac{1}{3}\,\,m/s\) theo phương vuông góc với sợi dây. Lực căng cực đại và cực tiểu của dây treo trong quá trình con lắc dao động là:
Vận tốc của con lắc ở vị trí cân bằng là:
\(\begin{gathered}
{v_{\max }} = \sqrt {2gl\left( {1 - \cos {\alpha _0}} \right)} \hfill \\
\Rightarrow \sqrt {2.10.1.\left( {1 - \cos {\alpha _0}} \right)} = \frac{1}{3} \hfill \\
\Rightarrow \cos {\alpha _0} = \frac{{179}}{{180}} \hfill \\
\end{gathered} \)
Lực căng cực đại và cực tiểu của dây treo là:
\(\begin{array}{*{20}{l}}
\begin{gathered}
{T_{\max }} = mg\left( {3 - 2\cos {\alpha _0}} \right) \hfill \\
= 0,15.10.\left( {3 - 2.\frac{{179}}{{180}}} \right) = 1,516\,\,\left( N \right) \hfill \\
\end{gathered} \\
\begin{gathered}
{T_{\min }} = mg\left( {3\cos {\alpha _0} - 2\cos {\alpha _0}} \right) \hfill \\
= 0,15.10.\left( {3.\frac{{179}}{{180}} - 2.\frac{{179}}{{180}}} \right) = 1,491\,\,\left( N \right) \hfill \\
\end{gathered}
\end{array}\)
Xét một con lắc đơn dao động với biên độ góc nhỏ. Mốc thế năng được chọn tại vị trí thấp nhất của vật nặng. Khi lực căng của dây treo có độ lớn bằng trọng lực của vật thì tỉ số giữa thế năng và động năng của vật \(\left( {\dfrac{{{W_t}}}{{{W_d}}}} \right)\) bằng bao nhiêu?
Lực căng dây của con lắc là:
\(\begin{array}{l}T = mg\left( {3\cos \alpha - 2\cos {\alpha _0}} \right) = mg\\ \Rightarrow 3\cos \alpha - 2\cos {\alpha _0} - 1 \Rightarrow \cos \alpha = \dfrac{{1 + 2\cos {\alpha _0}}}{3}\end{array}\)
Ta có tỉ số:
\(\begin{array}{l}\dfrac{{{{\rm{W}}_t}}}{{{{\rm{W}}_d}}} = \dfrac{{mgl\left( {1 - \cos \alpha } \right)}}{{mgl\left( {\cos \alpha - \cos {\alpha _0}} \right)}} = \dfrac{{1 - \cos \alpha }}{{\cos \alpha - \cos {\alpha _0}}}\\ \Rightarrow \dfrac{{{{\rm{W}}_t}}}{{{{\rm{W}}_d}}} = \dfrac{{1 - \dfrac{{1 + 2\cos {\alpha _0}}}{3}}}{{\dfrac{{1 + 2\cos {\alpha _0}}}{3} - \cos {\alpha _0}}} = \dfrac{{\dfrac{2}{3} - \dfrac{2}{3}\cos {\alpha _0}}}{{\dfrac{1}{3} - \dfrac{1}{3}\cos {\alpha _0}}} = 2\end{array}\)
Một con lắc đơn dao động với biên độ \({\alpha _0} < \dfrac{\pi }{2}\), có mốc thế năng được chọn tại vị trí cân bằng của vật nặng. Gọi độ lớn vận tốc của vật nặng khi động năng bằng thế năng là v1, khi độ lớn của lực căng dây treo bằng trọng lực tác động lên vật là v2 . Tỉ số \(\dfrac{{{v_1}}}{{{v_2}}}\) có giá trị nào sau đây?
+ Khi động năng bằng thế năng:
\(\begin{array}{l}{{\rm{W}}_t} = {\rm{W}} - {{\rm{W}}_t}\\ \Leftrightarrow mgl.\left( {1 - \cos {\alpha _1}} \right) = mgl.\left( {1 - \cos {\alpha _0}} \right) - mgl.\left( {1 - \cos {\alpha _1}} \right)\\ \Leftrightarrow 1 - \cos {\alpha _1} = \cos {\alpha _1} - \cos {\alpha _0}\\ \Leftrightarrow \cos {\alpha _1} = \dfrac{1}{2} + \dfrac{1}{2}.\cos {\alpha _0}\end{array}\)
+ Khi độ lớn của lực căng dây treo bằng trọng lực tác động lên vật:
\(\begin{array}{l}mg.\left( {3\cos {\alpha _2} - 2\cos {\alpha _0}} \right) = mg\\ \Leftrightarrow 3\cos {\alpha _2} - 2\cos {\alpha _0} = 1 \Leftrightarrow \cos {\alpha _2} = \dfrac{1}{3} + \dfrac{2}{3}.\cos {\alpha _0}\end{array}\)
+ Suy ra:
\(\begin{array}{l}\dfrac{{{v_1}}}{{{v_2}}} = \dfrac{{\sqrt {2gl\left( {\cos {\alpha _1} - \cos {\alpha _0}} \right)} }}{{\sqrt {2gl\left( {\cos {\alpha _2} - \cos {\alpha _0}} \right)} }} = \sqrt {\dfrac{{\cos {\alpha _1} - \cos {\alpha _0}}}{{\cos {\alpha _2} - \cos {\alpha _0}}}} \\\,\,\,\,\,\,\, = \sqrt {\dfrac{{\dfrac{1}{2} + \dfrac{1}{2}.\cos {\alpha _0} - \cos {\alpha _0}}}{{\dfrac{1}{3} + \dfrac{2}{3}.\cos {\alpha _0} - \cos {\alpha _0}}}} = \sqrt {\dfrac{{\dfrac{1}{2}\left( {1 - \cos {\alpha _0}} \right)}}{{\dfrac{1}{3}\left( {1 - \cos {\alpha _0}} \right)}}} = \sqrt {\dfrac{3}{2}} \end{array}\)
Con lắc đơn có chiều dài 1, vật nâng có khối lượng m = 200g. Từ vị trí cân bằng kéo vật sao cho dây treo hợp phương thẳng đúng góc \(\alpha = {60^0}\) rồi thả nhẹ. Bỏ qua lực ma sát và lực cản. Lấy gia tốc trọng trường\(g = 9,8m/{s^2}\). Trong quá trình chuyển động thì gia tốc tổng hợp có giá trị nhỏ nhất là:
Gia tốc pháp tuyến: \({a_n} = 2g\left( {\cos \alpha - \cos {\alpha _0}} \right)\)
Gia tốc tiếp tuyến: \({a_t} = g\sin \alpha \)
Gia tốc tổng hợp: \(a = \sqrt {a_n^2 + a_t^2} \Rightarrow a = g\sqrt {3{{\cos }^2}\alpha - 4\cos \alpha + 2} \)
\( \Rightarrow {a_{\min }} \Leftrightarrow {\left[ {\left( {3{{\cos }^2}\alpha - 4\cos \alpha + 2} \right)} \right]_{\min }}\)
\( \Rightarrow \cos \alpha = \frac{2}{3} \Rightarrow {a_{\min }} = g\sqrt {\frac{2}{3}} = 9,8\sqrt {\frac{2}{3}} = 8m/{s^2}\)

