Một mạch điện xoay chiều có u là điện áp tức thời ở hai đầu đoạn mạch và i là cường độ tức thời qua mạch. Chọn phát biểu đúng:
A - đúng
B, C, D - sai vì tùy loại mạch mà u và i có độ lệch pha khác nhau
Đặt điện áp u=U0cos(ωt) vào hai đầu cuộn cảm thuần có độ tự cảm L thì cường độ dòng điện qua cuộn cảm thuần là:
Ta có:
+ uL nhanh pha hơn i một góc π2
+ Cường độ dòng điện cực đại:
I0=U0ZL=U0ωL
=> Biểu thức cường độ dòng điện qua cuộn cảm thuần là:
i=U0ωLcos(ωt−π2)
Đặt vào hai đầu đoạn mạch chỉ có điện trở thuần R một điện áp xoay chiều có biểu thức u = U0cos(ωt) V thì cường độ dòng điện chạy qua điện trở có biểu thức i = I√2cos(ωt+ φi) A, trong đó I và φi được xác định bởi các hệ thức tương ứng là
Ta có:
+ Cường độ dòng điện hiệu dụng trong mạch chỉ có R:
I=UR=U0√2R
+ Cường độ dòng điện và hiệu điện thế trong mạch chỉ có R dao động cùng pha với nhau => φi = φu = 0
Đồ thị cường độ dòng điện như hình vẽ
Cường độ dòng điện tức thời có biểu thức
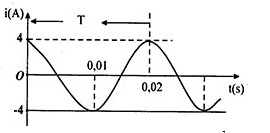
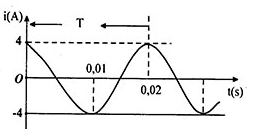
Từ đồ thị ta có:
+ Chu kì:
T=0,02s→ω=2πT=100π(rad/s)
+ Cường độ dòng điện cực đại:
I0=4(A)
+ Tại t = 0:
i=4↔I0cosφ=4→cosφ=1→φ=0
=> Biểu thức cường độ dòng điện tức thời:
i=4cos(100πt)A
Đoạn mạch điện xoay chiều gồm hai điện trở thuần R1 = 20 Ω và R2 = 40 Ω mắc nối tiếp với nhau. Đặt vào giữa hai đầu đoạn mạch một điện áp xoay chiều có biểu thức u = 120√2cos100πt V. Kết luận nào sau đây là không đúng ?
Ta có tổng trở của mạch: R = R1 + R2 = 60Ω
Cường độ dòng điện hiệu dụng trong mạch:
I=UR=12060=2A
Cường độ dòng điện cực đại qua R1 và R2 là như nhau và bằng:
I01=I02=I0=U0R=120√260=2√2A
Cường độ dòng điện và hiệu điện thế trong mạch dao động cùng pha nhau
=> Biểu thức cường độ dòng điện trong mạch:
i=2√2cos100πt
Mắc điện trở R=55Ωvào mạng điện xoay chiều có điện áp u=110cos(100πt+π/2)(V). Nhiệt lượng toả ra ở R trong 10 phút là:
Ta có, cường độ dòng điện cực đại trong mạch:
I0=U0R=11055=2A
Nhiệt lượng tỏa ra trên R trong 10 phút là:
Q=I2Rt=I20Rt2=22.55.10.602=66000J=66kJ
Một mạch điện xoay chiều nối tiếp có R=60Ω;L=0,2πH;C=10−4πF mắc vào mạng điện xoay chiều có chu kì 0,02s. Tổng trở của đoạn mạch là:
Ta có:
ω=2πT=2π0,02=100π(rad/s)R=60ΩZL=ωL=100π0,2π=20ΩZC=1ωC=1100π10−4π=100Ω
Tổng trở của mạch:
Z=√R2+(ZL−ZC)2=√602+(20−100)2=100Ω
Một cuộn dây thuần cảm có độ tự cảm L được mắc vào điện áp xoay chiều u có tần số f. Chọn phát biểu đúng:
A- sai vì: Cường độ dòng điện trong mạch chỉ có L trễ pha hơn điện áp u
B- đúng
C- sai vì:
I=UZL=UωL=U2πfL
=> cường độ dòng điện tỉ lệ nghịch với L và f
D- sai vì cường độ dòng điện biến thiên điều hòa với tần số f
Mạch nối tiếp gồm ampe kế, C=63,6μF,L=0,318H rồi mắc vào mạng điện xoay chiều (220V–50Hz). Số chỉ ampe kế là:
Ta có:
+ Hiệu điện thế hiệu dụng: U=220V
+ Cảm kháng:
ZL=ωL=2πfL=2π.50.0,318=100Ω
+ Dung kháng:
ZC=1ωC=12πfC=12π.50.63,6.10−6=50Ω
+ Tổng trở của mạch: Z=|ZL−ZC|=50Ω
Số chỉ ampe kế chính là cường độ dòng điện hiệu dụng:
I=UZ=22050=4,4(A)
Đồ thị biểu diễn cường độ tức thời của dòng điện xoay chiều chỉ có cuộn cảm thuần có cảm kháng ZL=50Ω như hình sau:
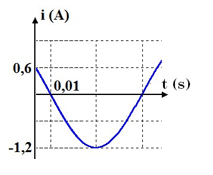
Viết biểu thức điện áp tức thời giữa hai đầu cuộn cảm.
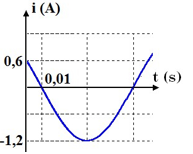
Từ đồ thị ta có:
T12=0,01s→T=0,12s→ω=2πT=50π3(rad/s)
+ Cường độ dòng điện cực đại:
I0=1,2(A)
+ Tại t=0: i=0,6A và đang giảm:
i=0,6↔I0cosφ=0,6→cosφ=0,61,2=12→φ=π3
=> Biểu thức cường độ dòng điện tức thời:
i=1,2cos(50π3t+π3)A
+ Ta có uL nhanh pha hơn i một góc π2
+ Hiệu điện thế cực đại:
U0=I0.ZL=1,2.50=60(V)
=> Biểu thức điện áp tức thời giữa hai đầu cuộn cảm:
u=60cos(50π3t+π3+π2)=60sin(50π3t+π3+π2+π2)=60sin(50π3t+4π3)V
Tác dụng của cuộn cảm đối với dòng điện xoay chiều là:
Ta có, cảm kháng:
ZL=2πfL
=> cảm kháng lớn nếu tần số dòng điện lớn
Đoạn mạch RLC nối tiếp. Biết điện áp tức thời ở hai đầu đoạn mạch sớm pha hơn cường độ dòng điện tức thời i chạy qua mạch 450. Chọn kết luận đúng:
Ta có :
+ u nhanh pha hơn i một góc 450
+ độ lệch pha giữa u và i được xác định bởi biểu thức :
tanφ=ZL−ZCR
→tanφ=ZL−ZCR=tanπ4→ZL−ZC=R
Một đoạn mạch điện xoay chiều gồm R=60Ω , cuộn cảm thuần L=0,2πH và C=10−38πF mắc nối tiếp. Điện áp giữa hai đầu đoạn mạch là u=100√2cos100πtV. Tìm độ lệch pha giữa điện áp giữa hai đầu đoạn mạch và dòng điện trong mạch?
Ta có:
ZL=ωL=100π0,2π=20Ω
ZC=1ωC=1100π.10−38π=80Ω
Độ lệch pha giữa điện áp và cường độ dòng điện trong mạch:
tanφ=ZL−ZCR=20−8060=−1→φ=−π4
Đoạn mạch điện xoay chiều chỉ có cuộn cảm có hệ số tự cảm L. Điện áp tức thời và cường độ dòng điện tức thời của mạch là u và i. Điện áp hiệu dụng và cường độ hiệu dụng là U,I. Biểu thức nào sau đây là đúng?
Mạch chỉ có cuộn cảm nên điện áp nhanh pha hơn dòng điện góc π2
Khi đó ta có
{u=UCcos(ωt+φu)=U√2cos(ωt+φu)i=I0cos(ωt+φu−π2)=I√2sin(ωt+φu)→(uU√2)2+(iI√2)2=1↔(uU)2+(iI)2=2
Mạch điện xoay chiều RLC nối tiếp. Biết điện áp tức thời giữa hai đầu đoạn mạch chậm pha hơn cường độ dòng điện tức thời là: 600 vàR=10√3Ω;ZL=50Ω. Dung kháng của tụ điện có giá trị là
Ta có, điện áp tức thời giữa hai đầu đoạn mạch chậm pha hơn cường độ dòng điện tức thời góc 600
→φ=−π3
Mặt khác, ta có:
tanφ=ZL−ZCR=tan(−π3)→ZL−ZC=−√3R→ZC=ZL+√3R=50+√3.10√3=80Ω
Điện áp của mạch điện xoay chiều là u=100√2cos(100πt+π2)V và cường độ dòng điện qua mạch là i=5√2cos(100πt+π3)A. Trong mạch điện có thể có:
Ta có:
u=100√2cos(100πt+π2)V và i=5√2cos(100πt+π3)A
=> Độ lệch pha giữa u và i:
φ=π2−π3=π6>0
Mặt khác, ta có:
tanφ=ZL−ZCR
=> Mạch có thể chứa R, L, C trong đó ZL > ZC hoặc mạch chỉ chứa R và L
Đặt điện áp xoay chiều vào hai đầu đọa mạch có R, L, C mắc nối tiếp. Khi trong đoạn mạch có cộng hưởng điện thì điện áp giữa hai đầu đoạn mạch
Khi trong mạch xảy ra hiện tượng cộng hưởng điện thì: ZL=ZC
=> điện áp giữa hai đầu đoạn mạch cùng pha với cường độ dòng điện trong mạch
Mạch điện xoay chiều chỉ có tụ điện với điện dung C. Đặt vào hai đầu tụ điện một điện áp u = U0cos(ωt + φ) V. Cường độ dòng điện hiệu dụng của mạch được cho bởi công thức:
Ta có: Cường độ dòng điện hiệu dụng trong mạch:
I=UZC=U1ωC=UωC=U0√2ωC
Cho đoạn mạch điện xoay chiều chỉ có tụ điện với điện dung C = 10−4π(F). Đặt điện áp xoay chiều có tần số 50Hz vào hai đầu đoạn mạch. Tại thời điểm mà điện áp hai đầu mạch có giá trị 100 √10 V thì cường độ dòng điện trong mạch là √2A. Điện áp hiệu dụng hai đầu tụ điện có giá trị là:
Dung kháng của mạch là :
ZC=1ωC=12π.50.10−4π=100Ω
Áp dụng hệ thức liên hệ ta được:
(uCU0C)2+(iI0)2=1↔(100√10100I0)2+(√2I0)2=1↔10I20+2I20=1→I0=2√3A→U0C=I0ZC=200√3V→UC=U0C√2=200√3√2=100√6V
Một học sinh mắc mạch điện như hình vẽ. Đặt vào A và B điện áp xoay chiều
u=U√2cos(100πt)
(U không đổi). Khi nối E, F với một ampe kế thì số chỉ của ampe kế là 3,8A. Khi nối E, F với một vôn kế thì số chỉ của vôn kế là 11,95V. Coi như hai cuộn dây thuần cảm và có hệ số tự cảm bằng nhau. Độ tự cảm cảu mỗi cuộn dây gần nhấu với giá trị nào sau đây?
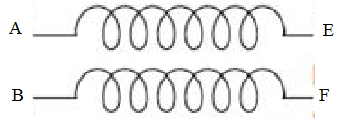
Khi mắc ampe kế vào E,F ta đo được cường độ dòng điện chạy trong mạch :
I=U2ZL⇒ZL=U2I
Khi mắc Vôn kế vào E, F thì ta đo được hiệu điện thế giữa hai điểm E, F tức là A, B (vì vôn kế lý tưởng và mạch thuần cảm). Vậy là U = 11,95V.
Lại có :
I=U2ZL⇒ZL=U2I=11,952.3,8=1,572Ω
Từ công thức tính cảm kháng ta có :
L=ZLω=1,572100π=5.10−3H=5mH

