Trên mặt nước có hai nguồn sóng nước giống nhau cách nhau AB=8(cm). Sóng truyền trên mặt nước có bước sóng 1,2(cm). Số đường cực đại đi qua đoạn thẳng nối hai nguồn là:
Do A,B dao động cùng pha nên số đường cực đại trên AB thoã mãn:
−Lλ<k<Lλ
Thay số ta có :
−81,2<k<81,2⇔−6,67<k<6,67
→k=±6,±5,±4,±3,±2,±1,0 .
Hai nguồn sóng cơ AB cách nhau dao động chạm nhẹ trên mặt chất lỏng, cùng tấn số 100Hz, cùng pha theo phương vuông vuông góc với mặt chất lỏng. Vận tốc truyền sóng 20m/s.Số điểm không dao động trên đoạn AB=1m là :
Ta có:
Bước sóng:
λ=vf=20100=0,2m
A, B dao động cùng pha => Số điểm không dao động (cực tiểu) trên AB thỏa mãn:
−Lλ−12<k<Lλ−12↔−10,2−12<k<10,2−12→−5,5<k<4,5→k=−5;±4,±3;±2;±1,0
=> Có 10 điểm
Có hiện tượng gì xảy ra khi một sóng mặt nước gặp một khe chắn hẹp có kích thước nhỏ hơn bước sóng?
Khi sóng mặt nước gặp một khe chắn hẹp có kích thước nhỏ hơn bước sóng thì sóng truyền qua khe giống như một tâm phát sóng mới
Hiện tượng giao thoa sóng là:
Hiện tượng giao thoa là hiện tượng hai sóng kết hợp khi gặp nhau thì có những điểm ở đó chúng luôn luôn tăng cường lẫn nhau, có những điểm ở đó chúng luôn luôn triệt tiêu nhau.
Tại hai điểm A,B trên mặt chất lỏng cách nhau 10(cm) có hai nguồn phát sóng theo phương thẳng đứng với các phương trình : u1=0,2.cos(50πt)cm vàu1=0,2.cos(50πt+π)cm . Vận tốc truyền sóng là 0,5 (m/s). Coi biên độ sóng không đổi. Xác định số điểm dao động với biên độ cực đại trên đoạn thẳng AB ?
Bước sóng :
λ=vT=v2πω=0,5.2π50π=0,02(m)=2cm.
Ta thấy A, B là hai nguồn dao động ngược pha nên số điểm dao động cực đại thoã mãn :
−ABλ−12<k<ABλ−12→−102−12<k<102−12→−5,5<k<4,5→k=−5;±4;±3;±2;±1;0.
=> Có 10 điểm
Phát biểu nào sau đây là không đúng?
A, B, C - đúng
D - sai vì: Các gợn sóng có hình các đường hypebol chứ không phải là đường thẳng
Trên mặt nước có hai nguồn kết hợp A,B cách nhau 10(cm) dao động theo các phương trình : u1=0,2.cos(50πt+π)cm và : u1=0,2.cos(50πt+π2)cm. Biết vận tốc truyền sóng trên mặt nước là 0,5(m/s). Tính số điểm cực đại và cực tiểu trên đoạn A,B.
Bước sóng :
λ=vT=v2πω=0,5.2π50π=0,02(m)=2cm
Nhìn vào phương trình ta thấy A,B là hai nguồn dao động vuông pha nên số điểm dao động cực đại và cực tiểu là bằng nhau và thoã mãn :
−ABλ−14<k<ABλ−14↔−102−14<k<102−14−5,25<k<4,75
=> Có 10 điểm dao động với biên độ cực đại và 10 điểm dao động cực tiểu.
Chọn câu trả lời đúng. Để phân loại sóng ngang hay sóng dọc người ta dựa vào:
Sóng dọc: là sóng trong đó các phần tử của môi trường dao động theo phương trùng với phương truyền sóng.
Sóng ngang: là sóng trong đó các phần tử của môi trường dao động theo phương vuông góc với phương truyền sóng.
=> Để phân biệt sóng ngang hay sóng dọc người ta dựa vào phương dao động và phương truyền sóng.
Một sóng hình sin truyền trên một sợi dây dài. Ở thời điểm t, hình dạng của một đoạn dây như hình vẽ. Các vị trí cân bằng của các phần tử trên dây cùng nằm trên trục Ox. Bước sóng của sóng này bằng:
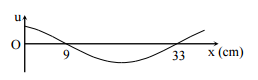
Từ đồ thị, ta có:
λ2=33−9=24cm→λ=48cm
Một âm có tần số xác định lần lượt truyền trong nhôm, nước, không khí với tốc độ tương ứng là v1,v2, v3. Nhận định nào sau đây là đúng
Tốc độ truyền sóng v: là tốc độ lan truyền dao động trong môi trường
Phụ thuộc vào bản chất của môi trường truyền (tính đàn hồi và mật độ môi trường): vR> vL> vK
=> v1> v2> v3
Trong thí nghiệm giao thoa sóng trên mặt nước, tốc độ truyền sóng là 0,5m/s, cần rung có tần số 40Hz. Khoảng cách giữa hai điểm cực đại giao thoa cạnh nhau trên đoạn thẳng S1S2.
Ta có: Bước sóng:
λ=vf=0,540=0,0125m=1,25cm
Khoảng cách giữa 2 cực đại liên tiếp :
λ2=1,252=0,625cm
Một nguồn dao động điều hoà với chu kỳ 0,04s. Vận tốc truyền sóng bằng 200cm/s. Hai điểm nằm trên cùng một phương truyền sóng và cách nhau 6 cm, thì có độ lệch pha:
Ta có:
Bước sóng:
λ=vT=200.0,04=8cm
Độ lệch pha của hai dao động tại hai điểm là:
Δφ=2πdλ=2π68=32π
Sóng cơ có tần số 50Hz truyền trong môi trường với vận tốc 160m/s. Ở cùng một thời điểm, hai điểm gần nhau nhất trên một phương truyền sóng có dao động cùng pha với nhau, cách nhau
Ta có bước sóng:
λ=vf=16050=3,2m
Khoảng cách giữa hai điểm gần nhau nhất trên một phương truyền sóng dao động cùng pha với nhau là 1 bước sóng.
Một sóng ngang truyền trên sợi dây đàn hồi rất dài với tần số 500Hz. Người ta thấy hai điểm A,B trên sợi dây cách nhau 200cm dao động cùng pha và trên đoạn dây AB có hai điểm khác dao động ngược pha với A. Tốc độ truyền sóng trên dây là:
2 điểm A, B dao động cùng pha và trên AB có 2 điểm khác dao động ngược pha với A.
→AB=2λ=200cm→λ=100cm
Ta có tốc độ truyền sóng:
v=λf=100.500=50000cm/s=500m/s
Trên bề mặt chất lỏng có hai nguồn kết hợp AB cách nhau 40cm dao động cùng pha. Biết sóng do mỗi nguồn phát ra có tần số f=10(Hz), vận tốc truyền sóng 2(m/s). Gọi M là một điểm nằm trên đường vuông góc với AB tại A và dao đông với biên độ cực đại. Đoạn AM có giá trị lớn nhất là :
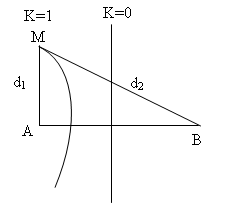
Ta có
λ=vf=20010=20(cm).
Do M là một cực đại giao thoa nên để đoạn AM có giá trị lớn nhất thì M phải nằm trên vân cực đại bậc 1 như hình vẽ và thõa mãn:
d2−d1=kλ=1.20=20(cm) (1). ( do lấy k = +1)
Mặt khác, do tam giác AMB là tam giác vuông tại A nên ta có :
BM=d2=√(AB2)+(AM2)=√402+d12(2)
Thay (2) vào (1) ta được :
√402+d12−d1=20⇒d1=30(cm)
Một sóng có tần số 500Hz và tốc độ lan truyền 350m/s. Hỏi hai điểm gần nhất trên phương truyền sóng cách nhau một khoảng bao nhiêu để giữa chúng có độ lệch pha π4?
Bước sóng:
λ=vf=350500=0,7m
Để độ lệch pha giữa 2 điểm gần nhất là π4
↔Δφ=2πdλ=π4→d=λ8=0,78=0,0875m=8,75cm
Chọn câu trả lời sai. Năng lượng của sóng truyền từ một nguồn điểm sẽ:
B - sai vì: Năng lượng sóng luôn không đổi khi môi trường truyền sóng là 1 đường thẳng
Một sợi dây đàn hồi rất dài có đầu A dao động với tần số f và theo phương vuông góc với sợi dây. Biên độ dao động là 4cm, vận tốc truyền sóng trên dây là 4(m/s). Xét một điểm M trên dây và cách A một đoạn 28cm, người ta thấy M luôn luôn dao động lệch pha với A một góc Δφ=(2k+1)π2 với k=0,±1,±2,..... Tính bước sóng λ? Biết tần số f có giá trị trong khoảng từ 22Hz đến 26Hz.
Độ lệch pha:
Δφ=(2k+1)π2=2πdλ→f=(2k+1)v4d
Mặt khác: 22Hz<f<26Hz
→22<f=(2k+1)v4d<26↔22<(2k+1)44.0,28<26→2,58<k<3,14→k=3→f=(2.3+1)44.0,28=25Hz→λ=vf=425=0,16m=16cm
Trên mặt chất lỏng có hai nguồn sóng dao động với cùng biên độ cùng tần số và cùng pha. Ta quan sát được hệ các vân đối xứng. Bây giờ nếu biên độ của một nguồn tăng lên gấp đôi nhưng vẫn dao động cùng pha với nguồn còn lại thì:
Giả sử ban đầu:
u1=u2=acos(ωt+φ)→{Amax=a1+a2=2aAmin
Nếu:
\left\{ \begin{array}{l}{u_1} = ac{\rm{os}}\left( {\omega t + \varphi } \right)\\{u_2} = 2{\rm{a}}c{\rm{os}}\left( {\omega t + \varphi } \right)\end{array} \right. \to \left\{ \begin{array}{l}{A_{{\rm{max}}}} = {a_1} + {a_2}' = a + 2{\rm{a}} = 3{\rm{a}}\\{A_{\min }} = \left| {{a_1} - {a_2}'} \right| = a\end{array} \right.
=> Nếu biên độ của một nguồn tăng lên gấp đôi nhưng vẫn dao động cùng pha với nguồn còn lại thì hiện tượng giao thao vẫn xảy ra, vị trí các vân không đổi nhưng vân cực tiểu lớn hơn và vân cực đại cũng lớn hơn
Một sóng ngang có chu kì T = 0,2s truyền trong một môi trường đàn hồi có tốc độ 1 m/s. Xét trên phương truyền sóng Ox, vào một thời điểm nào đó một điểm M nằm tại đỉnh sóng thì ở trước M theo chiều truyền sóng, cách M một khoảng từ 42cm đến 60cm có điểm N đang từ vị tri cân bằng đi lên đỉnh sóng . Khoảng cách MN là:
Bước sóng:
\lambda = vT = 1.0,2 = 0,2m
Độ lệch pha:
Khi điểm M ở đỉnh sóng, điểm N ở vị trí cân bằng đang đi lên
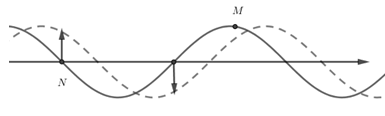
Theo hình vẽ thì khoảng cách MN
MN = \dfrac{3}{4}\lambda + k\lambda với k = 0; 1; 2; ...
\begin{array}{l}0,42 < MN = \dfrac{3}{4}\lambda + k\lambda < 0,60 \to 1,35 < k < 2,25\\ \to k = 2\\ \to MN = \dfrac{3}{4}\lambda + 2\lambda = 0,55m = 55cm\end{array}

