Hiện tượng quang điên - Thuyết lượng tử ánh sáng

Hiện tượng electron bị bật ra khỏi bề mặt kim loại khi có ánh sáng thích hợp chiếu vào gọi là hiện tượng quang điện ngoài.

Tia tử ngoại bị nước và thuỷ tinh hấp thụ mạnh.

Ta có :

${\rm{A}} = \dfrac{{{\rm{hc}}}}{{{{\rm{\lambda }}_0}}}{\rm{}} \to {{\rm{\lambda }}_0} = \dfrac{{{\rm{hc}}}}{{\rm{A}}} = 0,552{\rm{\mu m}}$

Để gây ra hiện tượng quang điện thì bức xạ chiếu đến có bước sóng nhỏ hơn λ₀ => bức xạ nào có thể gây ra hiện tượng quang điện là  λ₁ và λ₂

Với mỗi ánh sáng đơn sắc có tần số f, các photon đều giống nhau

Nhận thấy ánh sáng tím có bước sóng nằm trong khoảng từ $0,38\mu m - 0,42\mu m$

=> Phương án A: Ánh sáng tím có photon giống hệt nhau là sai

Ta có :  

$\left. \begin{gathered}\varepsilon  = hf = \frac{{hc}}{\lambda } \hfill \\{\lambda _{\text{D}}} > {\lambda _V} > {\lambda _L} \hfill \\\end{gathered}  \right\} \Rightarrow {\varepsilon _D} < {\varepsilon _V} < {\varepsilon _L}$

Năng lượng của bức xạ chiếu vào bề mặt tấm kim loại

 \(\varepsilon  = \dfrac{{hc}}{\lambda } = 3,76eV\)

Để xảy ra hiện tượng quang điện thì

\(\varepsilon  \geqslant A\)

Nhận thấy năng lượng photon của ánh sáng chiếu vào tấm kim loại lớn hơn công thoát của Kali và canxi. Do đó hiện tượng quang điện xảy ra đối với hai kim loại này.

Giới hạn quang điện của chất quang dẫn:

${\lambda _0} = 1,88\mu m = 1,{88.10^{ - 6}}m$

Tần số giới hạn quang điện của chất quang dẫn:

${f_0} = \dfrac{c}{{{\lambda _0}}} = 1,{596.10^{14}}Hz$

Điều kiện xảy ra hiện tượng quang điện trong:

$\lambda  \leqslant {\lambda _0} \Rightarrow f \geqslant {f_0} = 1,{596.10^{14}}Hz \Rightarrow {f_{\min }} = 1,{596.10^{14}}Hz$

Với tần số f thì: \(hf = A + K\) (1)

Với tần số 2f thì: \(2hf = A + K'\) (2)

(2) – (1) ta được: \(K' = {\text{ }}K + {\text{ }}hf\)

Ta giải hệ phương trình sau:

\(\left\{ \begin{gathered}\frac{{hc}}{{{\lambda _1}}} = A + \frac{1}{2}mv_1^2 \hfill \\\frac{{hc}}{{{\lambda _2}}} = A + \frac{1}{2}mv_2^2 \hfill \\\end{gathered}  \right.\Leftrightarrow \left\{ \begin{gathered}\frac{{hc}}{{{\lambda _1}}} = \frac{{hc}}{{{\lambda _0}}} + {K_1} \hfill \\\frac{{hc}}{{1,2{\lambda _1}}} = \frac{{hc}}{{{\lambda _0}}} + \frac{9}{{16}}{K_1} \hfill \\\end{gathered}  \right. \Rightarrow {\lambda _0} = 0,42\mu m\)

Năng lượng photon phát ra là:

\(\begin{array}{l}
\varepsilon = h{f_{nm}} = {E_n} - {E_m} = \left( { - 5,{{44.10}^{ - 19}}} \right)-\left( { - 21,{{76.10}^{ - 19}}} \right) = 16,{32.10^{ - 19}}J\\
\Rightarrow f = \frac{{{E_n} - {E_m}}}{h} = \frac{{16,{{32.10}^{ - 19}}}}{{6,{{625.10}^{ - 34}}}} = 2,{46.10^{15}}\left( {Hz} \right)
\end{array}\)

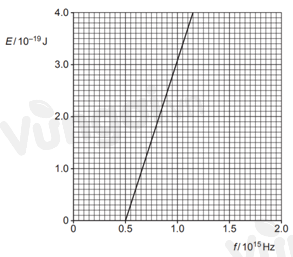
Từ đồ thị, lấy hai điểm ứng với E₁ = 0 có f₁ = 0,5.10¹⁵ Hz và E₂ = 4.10^-19 J có f₂ = 1,15.10¹⁵ Hz, ta có:

\(\left\{ \begin{array}{l}h{f_1} = h{f_0} + {E_1} \Rightarrow h{f_1} = h{f_0} \Rightarrow {f_0} = {f_1} = 0,{5.10^{15}}\,\,\left( {Hz} \right)\\h{f_2} = h{f_0} + {E_2} \Rightarrow h = \dfrac{{{E_2}}}{{{f_2} - {f_0}}} = \dfrac{{{{4.10}^{ - 19}}}}{{\left( {1,15 - 0,5} \right){{.10}^{15}}}} \approx 6,{2.10^{ - 34}}\,\,\left( {J/s} \right)\end{array} \right.\)

Electron chuyển động trong từ trường với quỹ đạo tròn có bán kính là:

\(r = \dfrac{{mv}}{{eB}} \Rightarrow v = \dfrac{{e.Br}}{m} = \dfrac{{1,{{6.10}^{ - 19}}.1,{{88.10}^{ - 4}}}}{{9,{{1.10}^{ - 31}}}} \approx {33.10^6}\,\,\left( {m/s} \right)\)

Áp dụng công thức Anh—xtanh về hiện tượng quang điện, ta có:

\(\begin{array}{l}\dfrac{{hc}}{\lambda } = A + \dfrac{1}{2}m{v_{0\max }}^2\\ \Rightarrow \dfrac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{{{{71.10}^{ - 12}}}} = A + \dfrac{1}{2}.9,{1.10^{ - 31}}.{\left( {{{33.10}^6}} \right)^2}\\ \Rightarrow A = 2,{3.10^{ - 15}}\,\,\left( J \right) = 14,4\,\,\left( {keV} \right)\end{array}\)

+ Năng lượng của 1 photon: \(\varepsilon  = \dfrac{{hc}}{\lambda }\)

\( \Rightarrow \) Năng lượng của \({30.10^{18}}{\mkern 1mu} {\mkern 1mu} photon\) là:  

\(A = {30.10^{18}}.\varepsilon  = {30.10^{18}}{\mkern 1mu} .\dfrac{{hc}}{\lambda }\,\,\,\left( J \right)\)

+ Năng lượng trung bình để đốt hoàn toàn \({\rm{1}}{\mkern 1mu} {\mkern 1mu} m{m^3}\) mô là \(2,53{\mkern 1mu} {\mkern 1mu} J\)
\( \Rightarrow \) Năng lượng cần thiết để đốt phần mô mềm có thể tích \(4{\mkern 1mu} {\mkern 1mu} m{m^3}\) là:

\(A' = 4.2,53 = 10,12J\)

+ Để đốt được phần mô mềm có thể tích \(4{\mkern 1mu} {\mkern 1mu} m{m^3}\) thì phần mô này cần hấp thụ hoàn toàn năng lượng của \({30.10^{18}}{\mkern 1mu} {\mkern 1mu} photon\) nên ta có:

\(\begin{array}{l}A = A' \Leftrightarrow 10,12 = {30.10^{18}}{\mkern 1mu} .\dfrac{{hc}}{\lambda }\\ \Leftrightarrow 10,12 = {30.10^{18}}.\dfrac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{\lambda }\\ \Rightarrow \lambda  = 5,{89.10^{ - 7}}{\mkern 1mu} {\mkern 1mu} \left( m \right) = 589{\mkern 1mu} {\mkern 1mu} \left( {nm} \right)\end{array}\)