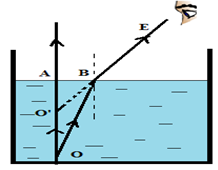
Một cái máng nước sâu 30 cm rộng 40 cm có hai thành bên thẳng đứng. Lúc máng cạn nước thì bóng râm của thành A kéo dài tới đúng chân thành B đối diện. Người ta đổ nước vào máng đến một độ cao h thì bóng của thành A ngắn bớt đi 7 cm so với trước. Biết chiết suất của nước là n = \(\frac{4}{3}\). h = ?
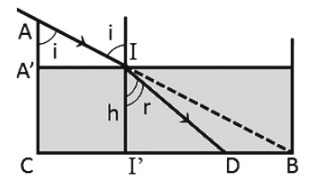
Ta có: \(\tan i = \frac{{CI'}}{{AA'}} = \frac{{CB}}{{AC}} = \frac{{40}}{{30}} = \frac{4}{3} \to i = {53,1^0}\)
Theo định luật khúc xạ ánh sáng, ta có:
\({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}} \to {\rm{sinr}} = \frac{{{n_1}\sin i}}{{{n_2}}} = \frac{{1.sin{{53,1}^0}}}{{\frac{4}{3}}} = 0,6 \to r = {36,87^0}\)
Mặt khác, từ hình ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}\tan i = \frac{{I'B}}{h}\\{\mathop{\rm t}\nolimits} {\rm{anr}} = \frac{{I'B - DB}}{h}\end{array} \right. \to \frac{{\tan i}}{{{\mathop{\rm t}\nolimits} {\rm{anr}}}} = \frac{{I'B}}{{I'B - DB}} = \frac{{16}}{9} \to I'B = \frac{{16}}{7}DB = \frac{{16}}{7}.7 = 16cm\\ \to h = \frac{{I'B}}{{\tan i}} = 12cm\end{array}\)
h = 12 (cm).
Trong hiện tượng khúc xạ
Trong hiện tượng khúc xạ ánh sáng:
+ Nếu n > 1: (môi trường khúc xạ (mt 2) chiết quang hơn môi trường tới (mt1))
\(\sin i > {\mathop{\rm s}\nolimits} {\rm{inr}} \to i > r\): tia khúc xạ gần pháp tuyến hơn so với tia tới
+ Nếu n < 1: (môi trường khúc xạ (mt 2) chiết quang kém môi trường tới (mt1))
\(\sin i < {\mathop{\rm s}\nolimits} {\rm{inr}} \to i < r\): tia khúc xạ xa pháp tuyến hơn so với tia tới
Một dây cọc dài được cắm thẳng đứng xuống một bể nước chiết suất \(\frac{4}{3}\). Phần cọc nhô ra ngoài mặt nước là 30cm, bóng của nó trên mặt nước dài 40cm và dưới đáy bể nước dài 190cm. Chiều sâu của lớp nước là:
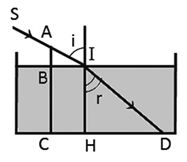
Theo đầu bài, ta có:
\(\left\{ \begin{array}{l}{n_1} = 1\\{n_2} = \frac{4}{3}\end{array} \right.;C{\rm{D}} = 190cm;BI = CH = 40cm;AB = 30cm\)
Từ hình vẽ, ta có:
\(\begin{array}{l}\tan i = \frac{{BI}}{{AB}} = \frac{{40}}{{30}} = \frac{4}{3} \to i = 53,{1^0}\\\end{array}\)
Theo định luật khúc xạ ánh sáng, ta có:
\({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}} \to {\rm{sinr}} = \frac{{{n_1}\sin i}}{{{n_2}}} = \frac{{1.\sin 53,1}}{{\frac{4}{3}}} = 0,6 \to r = 36,{87^0}\)
Mặt khác, từ hình ta có: \({\mathop{\rm t}\nolimits} {\rm{anr}} = \frac{{HD}}{{IH}} = \frac{{C{\rm{D}} - CH}}{{IH}} \to IH = \frac{{C{\rm{D}} - CH}}{{{\mathop{\rm t}\nolimits} {\rm{anr}}}} = \frac{{190 - 40}}{{0,75}} = 200cm\)
Khi chiếu tia sáng từ không khí đến mặt nước thì :
Khi chiếu sáng từ không khí đến mặt nước thì đồng thời có hiện tượng phản xạ và khúc xạ
Một thợ lặn dưới nước nhìn thấy Mặt Trời ở độ cao 600 so với đường chân trời. Độ cao thực của Mặt Trời (tạo một góc bao nhiêu độ so với đường chân trời) là bao nhiêu? Biết chiết suất của nước là 4/3
Ta có:
+ Góc tạo bởi Mặt Trời và phương ngang chính là góc của Mặt Trời so với đường chân trời
+ Vẽ hình ta được:
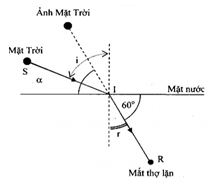
Từ hình, ta suy ra: Góc khúc xạ \(r = {90^0} - {60^0} = {30^0}\)
+ Vận dụng định luật khúc xạ, ta có:
\(\sin i = n{\mathop{\rm s}\nolimits} {\rm{inr}} \leftrightarrow \sin i = \frac{4}{3}\sin {30^0} \to \sin i = \frac{2}{3} \to i = 41,{8^0}\)
+ Góc mà Mặt Trời tạo với đường chân trời là: \(\alpha = {90^0} - 41,{8^0} \approx 48,{2^0}\)
Trong trường hợp sau đây, tia sáng không truyền thẳng khi
Trong các trường hợp trên, tia sáng không truyền thẳng khi truyền xiên góc từ không khí vào kim cương.
Chiếu chùm tia sáng đơn sắc từ không khí tới mặt phân cách của môi trường trong suốt có chiết suất n. Biết tia tới hợp với mặt phân cách góc 300. Khi đó tia khúc xạ hợp với mặt phân cách góc 600. Chiết suất n có giá trị bằng
Ta có:
Góc tới: \(i = {90^0} - {30^0} = {60^0}\)
Góc khúc xạ: \(r = {90^0} - {60^0} = {30^0}\)
Theo định luật khúc xạ ánh sáng, ta có: \({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}} \Leftrightarrow 1.\sin {60^0} = n\sin {30^0}\)
\( \Rightarrow n = \dfrac{{\sin {{60}^0}}}{{\sin {{30}^0}}} = \sqrt 3 \)
Tốc độ ánh sáng trong không khí là v1; trong nước là v2. Một tia sáng chiếu từ nước ra ngoài không khí với góc tới là i, có góc khúc xạ là r. Kết luận nào dưới đây là đúng?
Ta có tốc độ ánh sáng trong không khí lớn hơn tốc độ ánh sáng trong nước: \({v_1} > {v_2}\,\,\,\left( 1 \right)\)
Tia sáng truyền từ nước ra ngoài không khí. Áp dụng định luật khúc xạ ánh sáng ta có:
\(n\sin i = \sin \,r \Rightarrow i < r\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) ta có: \({v_1} > {v_2};i < r\)
Tia sáng đi từ không khí khi tới gặp mặt phân cách giữa không khí và môi trường trong suốt có chiết suất n = 1,5. Phải điều chỉnh góc tới đến giá trị nào thì góc tới gấp hai lần góc khúc xạ?
Hướng dẫn giải:
Theo định luật khúc xạ ánh sáng, ta có:
\({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}}\)
Theo đề bài: \(i{\rm{ }} = {\rm{ }}2r\)
\(1\sin i = 1,5{\mathop{\rm s}\nolimits} {\rm{in}}\frac{i}{2} \leftrightarrow 2\sin \frac{i}{2}{\rm{cos}}\frac{i}{2} = 1,5.\sin \frac{i}{2}\) (1)
Do \(i{\rm{ }} = {\rm{ }}2r\) nên \(i \ne 0\)
\( \to (1) \leftrightarrow 2c{\rm{os}}\frac{i}{2} = 1,5 \to c{\rm{os}}\frac{i}{2} = \frac{3}{4} \to \frac{i}{2} = 41,{4^0} \to i = 82,{8^0}\)
Trong các nhận định sau về hiện tượng khúc xạ, nhận định không đúng là
+ Tia khúc xạ nằm trong mặt phẳng chứa tia tới và pháp tuyến → A đúng
+ Tia khúc xạ nằm ở môi trường thứ 2 tiếp giáp với môi trường chứa tia tới → B đúng
+ Góc khúc xạ có thể lớn hơn, nhỏ hơn hoặc bằng góc tới (góc khúc xạ bằng góc tới khi góc khúc xạ bằng 0) → C đúng, D sai
Tốc độ truyền của ánh sáng trong môi trường nào sau đây là chậm nhất?
Tốc độ truyền ánh sáng là: \(v = \dfrac{c}{n} \Rightarrow v \sim \dfrac{1}{n}\)
Vậy tốc độ truyền ánh sáng chậm nhất trong môi trường có chiết suất lớn nhất
Một cái máng nước sâu 30 cm rộng 40 cm có hai thành bên thẳng đứng. Lúc máng cạn nước thì bóng râm của thành A kéo dài tới đúng chân thành B đối diện. Người ta đổ nước vào máng đến độ cao h bằng 2/3 độ cao của thành thì bóng của thành A ngắn bớt đi một đoạn d so với trước. Biết chiết suất của nước là \(n = \frac{4}{3}\). Xác định d.
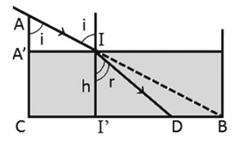
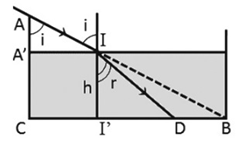
Từ hình vẽ ta thấy: \(\sin i = \frac{{A'I}}{{AI}} = \frac{{CB}}{{AB}} = \frac{{40}}{{\sqrt {{{30}^2} + {{40}^2}} }} = 0,8\)
\( \Rightarrow \frac{1}{{{{\sin }^2}i}} = 1 + \frac{1}{{{{\tan }^2}i}} \Rightarrow \frac{1}{{0,{8^2}}} = 1 + \frac{1}{{{{\tan }^2}i}} \Rightarrow \tan i = \frac{4}{3}\)
Áp dụng công thức định luật khúc xạ ánh sáng, ta có:
\(\sin i = n\sin r \Rightarrow \sin r = \frac{{\sin i}}{n} = \frac{{0,8}}{{\frac{4}{3}}} = 0,6\)
\( \Rightarrow \frac{1}{{{{\sin }^2}r}} = 1 + \frac{1}{{{{\tan }^2}r}} \Rightarrow \frac{1}{{0,{6^2}}} = 1 + \frac{1}{{{{\tan }^2}r}} \Rightarrow \tan r = 0,75\)
Lại có: \(h = II' = \frac{2}{3}AC = \frac{2}{3}.30 = 20{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)\)
Ta có:
\(\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{I'B = h.\tan i}\\{I'D = h.\tan r}\end{array}} \right. \Rightarrow d = I'B - I'D = h\left( {\tan i - \tan r} \right)}\\{ \Rightarrow d = 20.\left( {\frac{4}{3} - 0,75} \right) \approx 11,7{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)}\end{array}\)
Kẻ trộm giấu viên kim cương dưới đây một bể bơi, Anh ta đặt chiếc bè mỏng đồng chất hình tròn bán kính R trên mặt nước, tâm của bè nằm trên đường thẳng đứng đi qua viên kim vương. Mặt nước yên lặng và mức nước là 1,8m. Chiết suất của nước bằng 1,33. Giá trị nhỏ nhất của R để người ngoài bể bơi không nhìn thấy viên kim cương là:
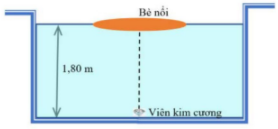
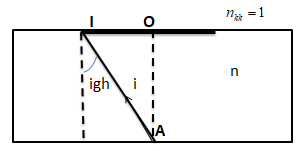
Để người ngoài bể bơi không quan sát thấy viên kim cương thì tia sáng từ viên kim cương đến mặt nước ngoài rìa của bè phải bị phản xạ toàn phần:
\(\sin {i_{gh}} = \frac{n}{{{n_{kk}}}} \Leftrightarrow \frac{R}{{\sqrt {{R^2} + 1,{8^2}} }} = \frac{1}{{1,33}}\)
\( \Leftrightarrow R = 2,05\left( m \right)\)
Một người nhìn thấy con cá ở trong nước. Hỏi muốn đâm trúng con cá thì người đó phải phóng mũi lao vào chỗ nào?
Gọi O là vị trí của con cá trong nước.
Do hiện tượng khúc xạ và do chiết suất của nước lớn hơn chiết suất của không khí nên ảnh của con cá sẽ ở vị trí O’ như hình vẽ.
Như vậy, người đó nhìn thấy con cá dường như gần mặt nước hơn. Để đâm trúng con cá thì người đó phải phóng mũi lao vào phía dưới vị trí mà người đó nhìn thấy con cá.