Cho tam giác $ABC$ có $BC = 11cm,\widehat {ABC} = 40^\circ $ và $\widehat {ACB} = {30^0}.$ Gọi $N$ là chân đường vuông góc hạ từ $A$ xuống cạnh $BC$.
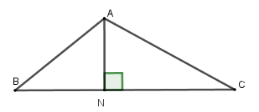
Độ dài $AC$ gần nhất với giá trị nào dưới đây ?
Theo câu trước ta có $AN \approx 3,76$;
Xét tam giác $ACN$ vuông tại $N$ có $\sin C = \dfrac{{AN}}{{AC}} \Rightarrow AC = \dfrac{{AN}}{{\sin C}} = 7,52$
Cho tam giác $ABC$ có $BC = 11cm,\widehat {ABC} = 40^\circ $ và $\widehat {ACB} = {30^0}.$ Gọi $N$ là chân đường vuông góc hạ từ $A$ xuống cạnh $BC$.

Diện tích tam giác $ABC$ gần với giá trị nào dưới đây ?
Theo kết quả các câu trước ta có $AN \approx 3,76$ nên ${S_{ABC}} = \dfrac{{AN.BC}}{2} = 20,68\,c{m^2}$.
Cho tam giác \(ABC\) cân tại \(A,\,\,\angle B = {65^0},\) đường cao \(CH = 3,6\). Hãy giải tam giác \(ABC\).
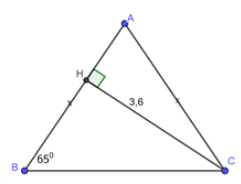
Vì \(\Delta ABC\) là tam giác cân tại \(A\)\( \Rightarrow \angle C = \angle B = {65^0}\)
Ta có \(\angle A + \angle B + \angle C = {180^0}\)(định lý tổng ba góc trong một tam giác)
\( \Rightarrow \angle A = {180^0} - 2\angle C = {180^0} - {2.65^0} = {50^0}\)
Xét \(\Delta ACH\) vuông tại \(H\) ta có:
\(\sin A = \dfrac{{CH}}{{AC}}\) \( \Leftrightarrow \sin {50^0} = \dfrac{{3,6}}{{AC}}\)\( \Rightarrow AC = \dfrac{{3,6}}{{\sin {{50}^0}}} \approx 4,7\)
Vì \(\Delta ABC\) là tam giác cân tại \(A\)\( \Rightarrow AC = AB \approx 4,7\)
Xét \(\Delta BCH\) vuông tại \(H\) ta có:
\(\sin B = \dfrac{{CH}}{{BC}} \Leftrightarrow \sin {65^0} = \dfrac{{3,6}}{{BC}} \)\(\Rightarrow BC = \dfrac{{3,6}}{{\sin {{65}^0}}} \approx 3,97\)
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\), biết \(HB = 9;HC = 16\). Tính góc \(B\) và góc \(C.\)
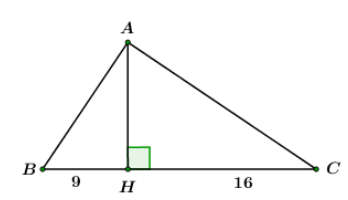
Ta có: \(BC = BH + CH = 9 + 16 = 25\)
Áp dụng hệ thức lượng cho \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\(A{B^2} = BH.BC\)\( \Leftrightarrow A{B^2} = 9.25 \Rightarrow AB = 15\)
\(A{C^2} = CH.BC\)\( \Leftrightarrow A{C^2} = 16.25 \Rightarrow AC = 20\)
Xét \(\Delta ABC\) vuông tại \(A\) ta có
\(\sin B = \dfrac{{AC}}{{BC}} = \dfrac{{20}}{{25}} = \dfrac{4}{5} \Rightarrow \angle B \approx {53^0}8'\)
\(\sin C = \dfrac{{AB}}{{BC}} = \dfrac{{15}}{{25}} = \dfrac{3}{5} \Rightarrow \angle C \approx {36^0}52'\)
Một tam giác cân có đường cao ứng với đáy đúng bằng độ dài đáy. Tính các góc của tam giác đó.
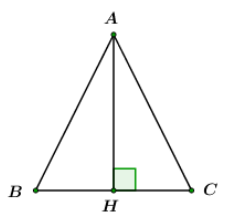
Giả sử \(BC = AH = a.\)
Vì \(\Delta ABC\) là tam giác cân nên \(AH\) là đường cao đồng thời là đường trung tuyến
\( \Rightarrow H\) là trung điểm \(BC\) \( \Rightarrow HB = HC = \dfrac{{BC}}{2} = \dfrac{a}{2}\)
Xét \(\Delta ABH\) vuông tại \(H\) ta có: \(tan\angle B = \dfrac{{AH}}{{BH}} = \dfrac{a}{{\dfrac{a}{2}}} = 2\) \( \Rightarrow \angle B \approx {63^0}26'\)
Vì \(\Delta ABC\) là tam giác cân\( \Rightarrow \angle C = \angle B \approx {63^0}26'\)
Ta có \(\angle A + \angle B + \angle C = {180^0}\) (định lý tổng ba góc trong một tam giác)
\( \Rightarrow \angle A = {180^0} - 2\angle C \approx {180^0} - {2.63^0}26' \approx {53^0}8'\)
Cho tam giác \(ABC\) vuông cân tại \(A\left( {AB = AC = a} \right)\) . Phân giác của góc \(B\) cắt \(AC\) tại \(D\).
Tính \(DA;DC\) theo \(a\).
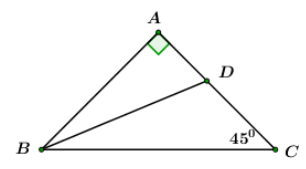
Vì tam giác \(ABC\) vuông cân tại \( \Rightarrow \angle B = \angle C = {45^0}\)
Vì \(BD\) là tia phân giác \(B\)
\( \Rightarrow \angle ABD = \angle DBC = \dfrac{1}{2}\angle B = \dfrac{{{{45}^0}}}{2} = 22,{5^0}\)
Xét \(\Delta ABD\) vuông tại \(A\) ta có
\(AD = AB.\tan \angle ABD = a.\tan 22,{5^0}\)
Ta có: \(AD + DC = AC\)\( \Rightarrow DC = AC - AD = a - a\tan 22,{5^0}\)
Cho hình thang \(ABCD\) vuông tại \(A\) và \(D;\)\(\angle C = {50^0}\). Biết \(AB = 2;AD = 1,2\). Tính diện tích hình thang \(ABCD.\)
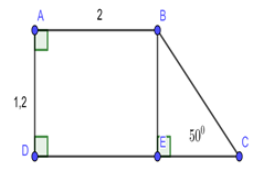
Kẻ \(BE \bot DC,\,\,\,E \in CD.\)
Xét tứ giác \(ABED\) có \(\angle A = \angle D = \angle E = {90^0}\)
\( \Rightarrow ABED\) là hình chữ nhật \( \Rightarrow \left\{ \begin{array}{l}AB = ED = 2\\AD = BE = 1,2\end{array} \right.\)
Xét \(\Delta BCE\) vuông tại \(E\) ta có: \(EC = BE.cot\angle C = 1,2.cot{50^0}\)
\( \Rightarrow DC = DE + EC = 2 + 1,2.\cot {50^0}\)
\( \Rightarrow {S_{ABCD}} = \dfrac{{\left( {AB + CD} \right)AD}}{2}\)\( = \dfrac{{\left( {2 + 2 + 1,2.\cot {{50}^0}} \right).1,2}}{2} \approx 3\,\,\,\,\left( {đvdt} \right).\)
Cho tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH.\) Biết \(AB = 3cm,\,\,AC = 4cm.\) Tính độ dài đường cao \(AH,\) tính \(\cos \angle ACB\).
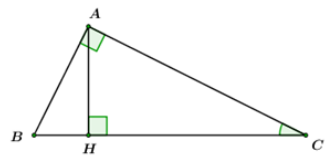
Áp dụng định lý Pitago trong \(\Delta ABC\) vuông tại \(A\) ta có: \(B{C^2} = A{C^2} + A{B^2} = {3^2} + {4^2} = {5^2} \Rightarrow BC = 5\,\,cm.\)
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\(AH.BC = AB.AC \Leftrightarrow AH = \dfrac{{AB.AC}}{{BC}} \)\(= \dfrac{{3.4}}{5} = 2,4cm.\)
Ta có: \(\cos \angle ACB = \dfrac{{AC}}{{BC}} = \dfrac{4}{5}.\)
Cho tam giác \(ABC\) vuông tại \(A\); \(BC = a\) không đổi, \(\angle C = \alpha \,\,\,\left( {{0^0} < \alpha < {{90}^0}} \right)\)
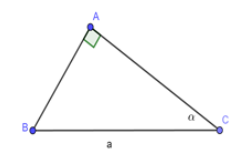
Lập công thức để tính diện tích tam giác ABC theo \(a\) và \(\alpha\) .
Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(\left\{ \begin{array}{l}AB = BC.\sin \alpha = a.\sin \alpha \\AC = BC.cos\alpha = a.cos\alpha \end{array} \right.\)
\({S_{ABC}} = \dfrac{1}{2}.AB.AC = \dfrac{1}{2}a.\sin \alpha .a.cos\alpha \)\(= \dfrac{1}{2}{a^2}.\sin \alpha .cos\alpha \)
Cho tam giác \(ABC\) vuông tại \(A\); \(BC = a\) không đổi, \(\angle C = \alpha \,\,\,\left( {{0^0} < \alpha < {{90}^0}} \right)\)

Tìm góc để diện tích tam giác ABC là lớn nhất. Tính giá trị lớn nhất ấy.
Áp dụng bất đẳng thức Cô-si ta có:
\({S_{ABC}} = \dfrac{1}{2}.AB.AC \le \dfrac{1}{2}.\dfrac{{\left( {A{B^2} + A{C^2}} \right)}}{2}\)\( = \dfrac{1}{4}.\left( {A{B^2} + A{C^2}} \right)\)
Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) ta có: \(A{B^2} + A{C^2} = B{C^2}\)
\( \Rightarrow {S_{ABC}} = \dfrac{1}{2}.AB.AC \le \dfrac{1}{4}.\left( {A{B^2} + A{C^2}} \right) = \dfrac{1}{4}B{C^2} = \dfrac{1}{4}{a^2}\)
Dấu “=” xảy ra \( \Leftrightarrow AC = AB\)\( \Leftrightarrow \Delta ABC\) vuông cân \( \Rightarrow \angle B = \angle C = {45^0}\) hay \(\alpha = {45^0}\).
Vậy \({S_{ABCmax}} = \dfrac{1}{4}{a^2}\) khi \(\alpha = {45^0}.\)

