Cho tam giác \(ABC\) vuông tại \(A\); \(BC = a\) không đổi, \(\angle C = \alpha \,\,\,\left( {{0^0} < \alpha  < {{90}^0}} \right)\)

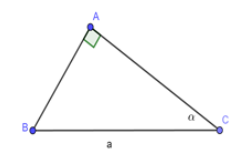
Tìm góc  để diện tích tam giác ABC là lớn nhất. Tính giá trị lớn nhất ấy.

Áp dụng bất đẳng thức Cô-si ta có:

\({S_{ABC}} = \dfrac{1}{2}.AB.AC \le \dfrac{1}{2}.\dfrac{{\left( {A{B^2} + A{C^2}} \right)}}{2}\)\( = \dfrac{1}{4}.\left( {A{B^2} + A{C^2}} \right)\)

Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) ta có: \(A{B^2} + A{C^2} = B{C^2}\)

\( \Rightarrow {S_{ABC}} = \dfrac{1}{2}.AB.AC \le \dfrac{1}{4}.\left( {A{B^2} + A{C^2}} \right) = \dfrac{1}{4}B{C^2} = \dfrac{1}{4}{a^2}\)

Dấu “=” xảy ra \( \Leftrightarrow AC = AB\)\( \Leftrightarrow \Delta ABC\) vuông cân  \( \Rightarrow \angle B = \angle C = {45^0}\) hay \(\alpha  = {45^0}\).

Vậy \({S_{ABCmax}} = \dfrac{1}{4}{a^2}\) khi \(\alpha  = {45^0}.\)