Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH.\) Biết \(AB = 3cm,\,\,AC = 4cm.\) Tính độ dài đường cao \(AH,\) tính \(\cos \angle ACB\).
Trả lời bởi giáo viên
Đáp án đúng: b
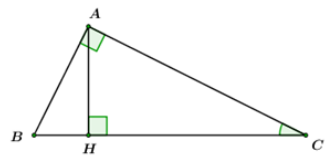
Áp dụng định lý Pitago trong \(\Delta ABC\) vuông tại \(A\) ta có: \(B{C^2} = A{C^2} + A{B^2} = {3^2} + {4^2} = {5^2} \Rightarrow BC = 5\,\,cm.\)
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\(AH.BC = AB.AC \Leftrightarrow AH = \dfrac{{AB.AC}}{{BC}} \)\(= \dfrac{{3.4}}{5} = 2,4cm.\)
Ta có: \(\cos \angle ACB = \dfrac{{AC}}{{BC}} = \dfrac{4}{5}.\)
Hướng dẫn giải:
Sử dụng hệ thức lượng trong tam giác vuông và công thức tỉ số lượng giác để làm bài toán.
Câu hỏi khác
- Bài tập một số hệ thức về cạnh và đường cao trong tam giác vuông toán 9 có lời giải
- Bài tập một số hệ thức về cạnh và góc trong tam giác vuông toán 9 có lời giải
- Bài tập tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập ứng dụng thực tế tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập hay và khó chương hệ thức lượng trong tam giác vuông toán 9 có lời giải
