Câu hỏi:
2 năm trước
Cho hình thang \(ABCD\) vuông tại \(A\) và \(D;\)\(\angle C = {50^0}\). Biết \(AB = 2;AD = 1,2\). Tính diện tích hình thang \(ABCD.\)
Trả lời bởi giáo viên
Đáp án đúng: b
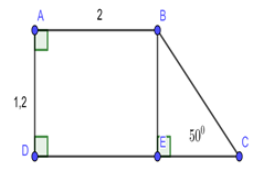
Kẻ \(BE \bot DC,\,\,\,E \in CD.\)
Xét tứ giác \(ABED\) có \(\angle A = \angle D = \angle E = {90^0}\)
\( \Rightarrow ABED\) là hình chữ nhật \( \Rightarrow \left\{ \begin{array}{l}AB = ED = 2\\AD = BE = 1,2\end{array} \right.\)
Xét \(\Delta BCE\) vuông tại \(E\) ta có: \(EC = BE.cot\angle C = 1,2.cot{50^0}\)
\( \Rightarrow DC = DE + EC = 2 + 1,2.\cot {50^0}\)
\( \Rightarrow {S_{ABCD}} = \dfrac{{\left( {AB + CD} \right)AD}}{2}\)\( = \dfrac{{\left( {2 + 2 + 1,2.\cot {{50}^0}} \right).1,2}}{2} \approx 3\,\,\,\,\left( {đvdt} \right).\)
Hướng dẫn giải:
Áp dụng hệ thức về cạnh và góc trong tam giác vuông.
Sử dụng tính chất hình chữ nhật.
Công thức tính diện tích hình thang vuông: \({S_{ABCD}} = \dfrac{{\left( {AB + CD} \right).AD}}{2}.\)
Câu hỏi khác
- Bài tập một số hệ thức về cạnh và đường cao trong tam giác vuông toán 9 có lời giải
- Bài tập một số hệ thức về cạnh và góc trong tam giác vuông toán 9 có lời giải
- Bài tập tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập ứng dụng thực tế tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập hay và khó chương hệ thức lượng trong tam giác vuông toán 9 có lời giải
