Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) vuông tại \(A\); \(BC = a\) không đổi, \(\angle C = \alpha \,\,\,\left( {{0^0} < \alpha < {{90}^0}} \right)\)
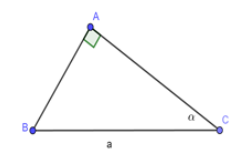
Lập công thức để tính diện tích tam giác ABC theo \(a\) và \(\alpha\) .
Trả lời bởi giáo viên
Đáp án đúng: a
Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(\left\{ \begin{array}{l}AB = BC.\sin \alpha = a.\sin \alpha \\AC = BC.cos\alpha = a.cos\alpha \end{array} \right.\)
\({S_{ABC}} = \dfrac{1}{2}.AB.AC = \dfrac{1}{2}a.\sin \alpha .a.cos\alpha \)\(= \dfrac{1}{2}{a^2}.\sin \alpha .cos\alpha \)
Hướng dẫn giải:
Áp dụng hệ thức về cạnh và góc trong tam giác vuông.
Sử dụng công thức tính diện tích tam giác \({S_{ABC}} = \dfrac{1}{2}AB.AC.\)
Câu hỏi khác
- Bài tập một số hệ thức về cạnh và đường cao trong tam giác vuông toán 9 có lời giải
- Bài tập một số hệ thức về cạnh và góc trong tam giác vuông toán 9 có lời giải
- Bài tập tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập ứng dụng thực tế tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập hay và khó chương hệ thức lượng trong tam giác vuông toán 9 có lời giải
