Một tam giác cân có đường cao ứng với đáy đúng bằng độ dài đáy. Tính các góc của tam giác đó.

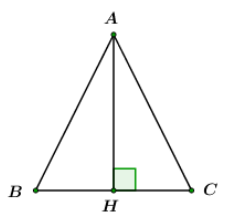
Giả sử \(BC = AH = a.\) 

Vì \(\Delta ABC\) là tam giác cân nên \(AH\) là đường cao đồng thời là đường trung tuyến

\( \Rightarrow H\) là trung điểm \(BC\) \( \Rightarrow HB = HC = \dfrac{{BC}}{2} = \dfrac{a}{2}\)

Xét \(\Delta ABH\) vuông tại \(H\) ta có:  \(tan\angle B = \dfrac{{AH}}{{BH}} = \dfrac{a}{{\dfrac{a}{2}}} = 2\) \( \Rightarrow \angle B \approx {63^0}26'\)

Vì \(\Delta ABC\) là tam giác cân\( \Rightarrow \angle C = \angle B \approx {63^0}26'\)

Ta có \(\angle A + \angle B + \angle C = {180^0}\) (định lý tổng ba góc trong một tam giác)

\( \Rightarrow \angle A = {180^0} - 2\angle C \approx {180^0} - {2.63^0}26' \approx {53^0}8'\)