Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\), biết \(HB = 9;HC = 16\). Tính góc \(B\) và góc \(C.\)
Trả lời bởi giáo viên
Đáp án đúng: a
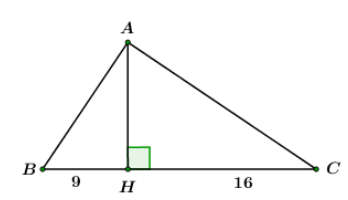
Ta có: \(BC = BH + CH = 9 + 16 = 25\)
Áp dụng hệ thức lượng cho \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\(A{B^2} = BH.BC\)\( \Leftrightarrow A{B^2} = 9.25 \Rightarrow AB = 15\)
\(A{C^2} = CH.BC\)\( \Leftrightarrow A{C^2} = 16.25 \Rightarrow AC = 20\)
Xét \(\Delta ABC\) vuông tại \(A\) ta có
\(\sin B = \dfrac{{AC}}{{BC}} = \dfrac{{20}}{{25}} = \dfrac{4}{5} \Rightarrow \angle B \approx {53^0}8'\)
\(\sin C = \dfrac{{AB}}{{BC}} = \dfrac{{15}}{{25}} = \dfrac{3}{5} \Rightarrow \angle C \approx {36^0}52'\)
Hướng dẫn giải:
Áp dụng hệ thức về cạnh và góc trong tam giác vuông
Từ tỉ số lượng giác suy ra số đo góc
Sử dụng hệ thức lượng trong tam giác vuông: \(A{B^2} = BH.BC\); \(A{C^2} = CH.BC\)
Câu hỏi khác
- Bài tập một số hệ thức về cạnh và đường cao trong tam giác vuông toán 9 có lời giải
- Bài tập một số hệ thức về cạnh và góc trong tam giác vuông toán 9 có lời giải
- Bài tập ứng dụng thực tế tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập hay và khó chương hệ thức lượng trong tam giác vuông toán 9 có lời giải
