Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 26\,cm,AB = 10\,cm\) Tính \(AC;\widehat B\) . (làm tròn đến độ)
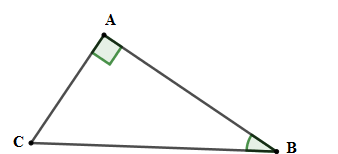
Xét tam giác \(ABC\) vuông tại \(A\) có
+) \(B{C^2} = A{B^2} + A{C^2} \Rightarrow AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{26}^2} - {{10}^2}} = 24\)
+) \(\sin B = \dfrac{{AC}}{{BC}} = \dfrac{{24}}{{26}} = \dfrac{{12}}{{13}} \Rightarrow \widehat B \approx 67^\circ \)
Vậy \(AC = 24;\widehat C \approx 67^\circ \).
Diện tích tam giác \(ABC\) gần nhất với giá trị nào dưới đây ?
Theo các câu trước ta có \(AN \approx 2,79\) nên \({S_{ABC}} = \dfrac{{AN.BC}}{2} = 12,555\,c{m^2}\).
Độ dài \(AC\) gần nhất với giá trị nào dưới đây ?
Theo câu trước ta có \(AN \approx 2,79\);
Xét tam giác \(ACN\) vuông tại \(N\) có \(\sin C = \dfrac{{AN}}{{AC}} \Rightarrow AC = \dfrac{{AN}}{{\sin C}} \approx 4,87\)
Độ dài \(AN\) gần nhất với giá trị nào dưới đây ?
Đặt \(BN = x\,\left( {0 < x < 9} \right)\)\( \Rightarrow NC = 9 - x\)
Xét tam giác \(ABN\) vuông tại \(N\) có \(AN = BN.\tan B = x.\tan 50^\circ \)
Xét tam giác \(ACN\) vuông tại \(N\) có \(AN = CN.\tan B = \left( {9 - x} \right).\tan 35^\circ \)
Nên \(x\tan 50^\circ = \left( {9 - x} \right)\tan 35^\circ \Rightarrow x \approx 3,33\) (thoả mãn)
Khi đó \(AN = BN.\tan B = 3,33.\tan 40^\circ \approx 2,79\)
Độ dài \(AN\) gần nhất với giá trị nào dưới đây ?
Đặt \(BN = x\,\left( {0 < x < 9} \right)\)\( \Rightarrow NC = 9 - x\)
Xét tam giác \(ABN\) vuông tại \(N\) có \(AN = BN.\tan B = x.\tan 50^\circ \)
Xét tam giác \(ACN\) vuông tại \(N\) có \(AN = CN.\tan B = \left( {9 - x} \right).\tan 35^\circ \)
Nên \(x\tan 50^\circ = \left( {9 - x} \right)\tan 35^\circ \Rightarrow x \approx 3,33\) (thoả mãn)
Khi đó \(AN = BN.\tan B = 3,33.\tan 40^\circ \approx 2,79\)
Cho tam giác \(ABC\) có \(AB = 12,AC = 15\) và \(\widehat B = {60^0}\). Tính \(BC\)
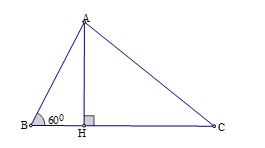
Kẻ đường cao \(AH\).
Xét tam giác vuông \(ABH\), ta có: \(BH = AB.\cos B = AB.\cos {60^0} = 12.\dfrac{1}{2} = 6\)\(AH = AB.\sin B = AB.\sin {60^0} = 12.\dfrac{{\sqrt 3 }}{2} = 6\sqrt 3 \).
Áp dụng định lý Pythago vào tam giác vuông \(AHC\) ta có:
\(H{C^2} = A{C^2} - A{H^2} = {15^2} - {\left( {6\sqrt 3 } \right)^2} = 117\). Suy ra \(HC = 3\sqrt {13} \). Vậy \(BC = CH + HB = 3\sqrt {13} + 6\).
Cho tam giác \(ABC\) có \(\widehat B = {70^0},\widehat C = {35^0},AC = 4,5cm.\) Diện tích tam giác \(ABC\) gần nhất với giá trị nào dưới đây? (làm tròn đến chữ số thập phân thứ hai)
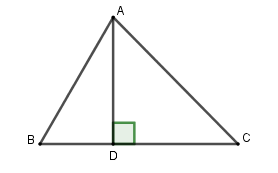
Kẻ đường cao \(AD\).
Xét tam giác vuông \(ACD\), có \(AD = AC.\sin C = 4,5.\sin 35^\circ \approx 2,58\,cm\); \(CD = AC.\cos C = 4,5.\cos 35^\circ \approx 3,69\,cm\)
Xét tam giác vuông \(ABD\), có \(BD = AD.\cot B \approx 2,58.\cot 70^\circ \approx 0,94\,cm\)
Suy ra \(BC = BD + DC = 0,94 + 3,69 = 4,63\)
Do đó \({S_{ABC}} = \dfrac{{AD.BC}}{2} \approx 5,97\)\(c{m^2}\).
Cho tứ giác \(ABCD\) có \(\widehat A = \widehat D = {90^0},\widehat C = {45^0},AB = 6cm,AD = 8cm.\) Tính diện tích tứ giác \(ABCD.\)
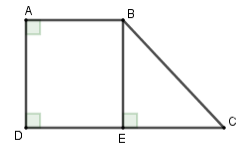
Vì \(\widehat A = \widehat D = {90^0} \Rightarrow AD{\rm{//}}BC\) hay \(ABCD\) là hình thang vuông tại \(A,D\)
Kẻ \(BE \bot DC\) tại \(E\).
Tứ giác \(ABED\) có ba góc vuông \(\widehat A = \widehat D = \widehat E = 90^\circ \) nên \(ABED\) là hình chữ nhật
Suy ra \(DE = AB = 6\,\,cm;BE = AD = 8\,cm\)
Xét tam giác \(BEC\) vuông tại \(E\) có \(\widehat {BCE} = 45^\circ \) nên tam giác \(BEC\) vuông cân tại \(E\) \( \Rightarrow EC = BE = 8cm \Rightarrow DC = DE + EC = 6 + 8 = 14cm\)
Do đó \({S_{ABCD}} = \dfrac{{\left( {AB + CD} \right).AD}}{2} = \dfrac{{\left( {6 + 14} \right)8}}{2} = 80\,\,c{m^2}\).
Cho tam giác $MNP$ vuông tại $N$. Hệ thức nào sau đây là đúng?
Ta có $\sin P = \dfrac{{MN}}{{MP}} \Rightarrow MN = MP.\sin P$.
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = a,AC = b,AB = c.\) Chọn khẳng định sai?
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = a,AC = b,AB = c.\) Ta có :
+) Theo định lý Py-ta-go ta có ${a^2} = {b^2} + {c^2}$ nên C đúng
+) Theo hệ thức về cạnh và góc trong tam giác vuông ta có
\(b = a.\sin B = a.\cos C\); \(c = a.\sin C = a.\cos B\); \(b = c.\tan B = c.\cot C\); \(c = b.\tan C = b.\cot B\).
Nên A,D đúng.
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 10\,cm,\widehat C = 30^\circ .\) Tính $AB;BC$
Xét tam giác \(ABC\) vuông tại \(A\) có
$\tan C = \dfrac{{AB}}{{AC}} \Rightarrow AB = AC.\tan C = 10.\tan 30^\circ = \dfrac{{10\sqrt 3 }}{3}$; $\cos C = \dfrac{{AC}}{{BC}} \Rightarrow BC = \dfrac{{AC}}{{\cos C}} = \dfrac{{10}}{{\dfrac{{\sqrt 3 }}{2}}} = \dfrac{{20\sqrt 3 }}{3}$
Vậy $AB = \dfrac{{10\sqrt 3 }}{3};BC = \dfrac{{20\sqrt 3 }}{3}$.
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 12\,cm,\widehat B = 40^\circ .\) Tính $AC;\widehat C$ . (làm tròn đến chữ số thập phân thứ hai)
Xét tam giác \(ABC\) vuông tại \(A\) có
+) $\sin B = \dfrac{{AC}}{{BC}} \Rightarrow AC = BC.\sin B = 12.\sin 40^\circ \approx 7,71$
+) $\widehat A + \widehat B + \widehat C = 180^\circ \Rightarrow \widehat C = 180^\circ - 40^\circ - 90^\circ = 50^\circ $
Vậy $AC \approx 7,71;\widehat C = 50^\circ $.
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 15\,cm,AB = 12\,cm\) . Tính $AC;\widehat B$ .
Xét tam giác \(ABC\) vuông tại \(A\) có
+) $B{C^2} = A{B^2} + A{C^2} \Rightarrow AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{15}^2} - {{12}^2}} = 9 (cm)$
+) $\sin B = \dfrac{{AC}}{{BC}} = \dfrac{9}{{15}} = \dfrac{3}{5}$
$\Rightarrow \widehat B \approx 36^\circ 52'$
Vậy $AC = 9 (cm);\widehat B \approx 36^\circ 52'$.
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 7\,cm,AB = \,5cm\). Tính $BC;\widehat C$ .
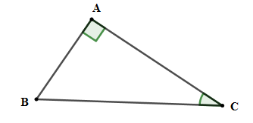
Xét tam giác \(ABC\) vuông tại \(A\) có
+) $B{C^2} = A{B^2} + A{C^2} = {5^2} + {7^2} = 74 \Rightarrow BC = \sqrt {74} (cm)$
+) $\tan C = \dfrac{{AB}}{{AC}} = \dfrac{5}{7} \Rightarrow \widehat C \approx 35^\circ 32'$
Vậy $BC = \sqrt {74}(cm) ;\widehat C \approx 35^\circ 32'$.
Cho tam giác \(ABC\) có \(AB = 16,AC = 14\) và \(\widehat B = {60^0}\). Tính $BC$
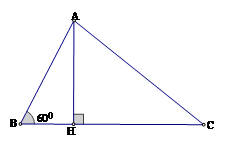
Kẻ đường cao \(AH\).
Xét tam giác vuông \(ABH\), ta có: \(BH = AB.\cos B = AB.\cos {60^0} = 16.\dfrac{1}{2} = 8\)\(AH = AB.\sin B = AB.\sin {60^0} = 16.\dfrac{{\sqrt 3 }}{2} = 8\sqrt 3 \).
Áp dụng định lý Pythago vào tam giác vuông \(AHC\) ta có:
\(H{C^2} = A{C^2} - A{H^2} = {14^2} - {\left( {8\sqrt 3 } \right)^2} = 196 - 192 = 4\). Suy ra \(HC = 2\). Vậy \(BC = CH + HB = 2 + 8 = 10\).
Cho tam giác $ABC$ có $\widehat B = {60^0},\widehat C = {50^0},AC = 3,5cm.$ Diện tích tam giác $ABC$ gần nhất với giá trị nào dưới đây?
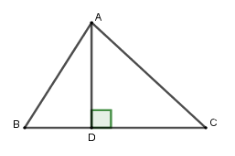
Kẻ đường cao \(AD\).
Xét tam giác vuông \(ACD\), có $AD = AC.\sin C = 3,5.\sin 50^\circ \approx 2,68\,cm$; $CD = AC.\cos C = 3,5.\cos 50^\circ \approx 2,25\,\,cm$
Xét tam giác vuông \(ABD\), có $BD = AD.\cot B \approx 2,68.\cot 60^\circ \approx 1,55\,\,cm$
Suy ra $BC = BD + CD = 3,8$
Do đó ${S_{ABC}} = \dfrac{{AD.BC}}{2} \approx 5,09$$c{m^2}$.
Cho tứ giác $ABCD$ có $\widehat A = \widehat D = {90^0},\widehat C = {40^0},AB = 4cm,AD = 3cm.$ Tính diện tích tứ giác $ABCD.$ (làm tròn đến chữ số thập phân thứ hai)
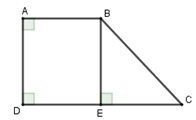
Vì $\widehat A = \widehat D = {90^0} \Rightarrow AD{\rm{//}}BC$ hay $ABCD$ là hình thang vuông tại $A,D$
Kẻ $BE \bot DC$ tại $E$.
Tứ giác $ABED$ có ba góc vuông $\widehat A = \widehat D = \widehat E = 90^\circ $ nên $ABED$ là hình chữ nhật
Suy ra $DE = AB = 4\,\,cm;BE = AD = 3\,cm$
Xét tam giác $BEC$ vuông tại $E$ có $EC = BE.\cot 40^\circ=3.\cot40^0 $ $\Rightarrow DC = DE + EC =4+3.\cot40^0$
Do đó ${S_{ABCD}} = \dfrac{{\left( {AB + CD} \right).AD}}{2}$\(=\dfrac{(4+4+3.\cot40^0).3}{2}\)
$\approx 17,36\,\,c{m^2}$.
Cho tam giác \(DEF\) có \(DE = 7cm;\angle D = {40^0};\angle F = {58^0}\). Kẻ đường cao \(EI\) của tam giác đó.
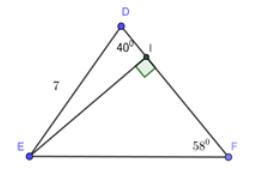
Hãy tính: (Kết quả làm tròn đến chữ số thập phân thứ 1)
Đường cao \(EI\)
Xét \(\Delta DEI\) vuông tại \(I\) ta có: \(EI = ED.\sin D = 7.\sin {40^0}\)\( \approx 4,5\,\,cm.\)
Cho tam giác \(DEF\) có \(DE = 7cm;\angle D = {40^0};\angle F = {58^0}\). Kẻ đường cao \(EI\) của tam giác đó.

Hãy tính: (Kết quả làm tròn đến chữ số thập phân thứ 1)
Cạnh \(EF\)
Xét \(\Delta EIF\) vuông tại \(I\) ta có:
\(EI = EF.\sin F \Leftrightarrow EF = \dfrac{{EI}}{{\sin F}} \approx \dfrac{{4,5}}{{\sin {{58}^0}}} \approx 5,3\,cm.\)
Cho tam giác $ABC$ có $BC = 11cm,\widehat {ABC} = 40^\circ $ và $\widehat {ACB} = {30^0}.$ Gọi $N$ là chân đường vuông góc hạ từ $A$ xuống cạnh $BC$.
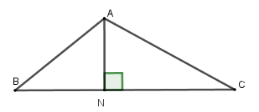
Độ dài $AN$ gần nhất với giá trị nào dưới đây ?
Đặt $BN = x\,\left( {0 < x < 11} \right)$$ \Rightarrow NC = 11 - x$
Xét tam giác $ABN$ vuông tại $N$ có $AN = BN.\tan B = x.\tan 40^\circ $
Xét tam giác $ACN$ vuông tại $N$ có $AN = CN.\tan C = \left( {11 - x} \right).\tan 30^\circ $
Nên $x\tan 40^\circ = \left( {11 - x} \right)\tan 30^\circ $
$\Rightarrow x \approx 4,48 $ (thoả mãn)
Khi đó $AN = BN.\tan B = 4,48.\tan 40^\circ \approx 3,76(cm).$

